numpy.random.zipf#

random.zipf(a, size=None)#

从齐普夫（Zipf）分布中抽取样本。

样本是从指定参数 a > 1 的齐普夫（Zipf）分布中抽取的。

齐普夫（Zipf）分布（也称为 zeta 分布）是一种满足齐普夫定律的离散概率分布：项目的频率与其在频率表中的排名成反比。

注意

新代码应该使用 zipf 方法，该方法属于 Generator 实例；请参阅快速入门。

参数:

a浮点数或浮点数数组: 分布参数。必须大于 1。
size整数或整数元组，可选: 输出形状。如果给定的形状是，例如，(m, n, k)，则抽取 m * n * k 个样本。如果 size 为 None （默认值），如果 a 是一个标量，则返回单个值。否则，将抽取 np.array(a).size 个样本。

返回:

outndarray 或标量: 从参数化齐普夫（Zipf）分布中抽取的样本。

另请参阅

scipy.stats.zipf: 概率密度函数、分布或累积密度函数等。
random.Generator.zipf: 新代码应使用此方法。

注释

齐普夫（Zipf）分布的概率质量函数（PMF）为

\[p(k) = \frac{k^{-a}}{\zeta(a)},\]

对于整数 \(k \geq 1\)，其中 \(\zeta\) 是黎曼 zeta 函数。

它以美国语言学家乔治·金斯利·齐普夫（George Kingsley Zipf）的名字命名，他指出任何单词在语言样本中的出现频率与其在频率表中的排名成反比。

参考

[1]

Zipf, G. K., “Selected Studies of the Principle of Relative Frequency in Language,” Cambridge, MA: Harvard Univ. Press, 1932.

示例

从分布中抽取样本

>>> a = 4.0
>>> n = 20000
>>> s = np.random.zipf(a, n)

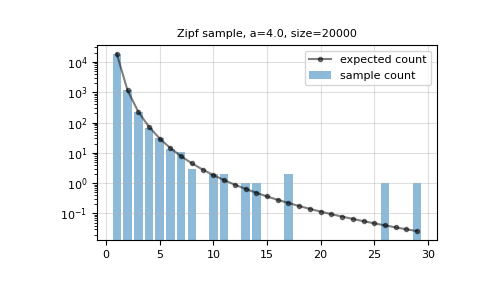
显示样本的直方图，以及基于概率密度函数的预期直方图

>>> import matplotlib.pyplot as plt
>>> from scipy.special import zeta  

bincount 为小整数提供了快速直方图。

>>> count = np.bincount(s)
>>> k = np.arange(1, s.max() + 1)

>>> plt.bar(k, count[1:], alpha=0.5, label='sample count')
>>> plt.plot(k, n*(k**-a)/zeta(a), 'k.-', alpha=0.5,
...          label='expected count')   
>>> plt.semilogy()
>>> plt.grid(alpha=0.4)
>>> plt.legend()
>>> plt.title(f'Zipf sample, a={a}, size={n}')
>>> plt.show()

../../../_images/numpy-random-zipf-1.png