numpy.random.RandomState.wald#

方法

random.RandomState.wald(mean, scale, size=None)#

从 Wald 分布（也称为逆高斯分布）中抽取样本。

当 scale 接近无穷大时，该分布变得更像高斯分布。一些参考文献声称 Wald 是一个均值等于 1 的逆高斯分布，但这绝不是普遍的。

逆高斯分布最初是研究布朗运动时提出的。1956 年，M.C.K. Tweedie 使用了逆高斯这个名称，因为覆盖单位距离的时间与单位时间内覆盖的距离之间存在反比关系。

注意

新代码应使用 wald 方法，该方法属于 Generator 实例；请参阅快速入门。

参数:

mean浮点数或浮点数的类数组对象: 分布均值，必须 > 0。
scale浮点数或浮点数的类数组对象: 尺度参数，必须 > 0。
sizeint 或 int 元组，可选: 输出形状。如果给定的形状是，例如，(m, n, k)，则抽取 m * n * k 个样本。如果 size 是 None（默认值），则如果 mean 和 scale 都是标量，则返回单个值。否则，抽取 np.broadcast(mean, scale).size 个样本。

返回:

参见

备注

Wald 分布的概率密度函数为

\[P(x;mean,scale) = \sqrt{\frac{scale}{2\pi x^3}}e^ \frac{-scale(x-mean)^2}{2\cdotp mean^2x}\]

如上所述，逆高斯分布最初出现在尝试模拟布朗运动的尝试中。它也是用于可靠性建模以及对股票收益率和利率过程建模的 Weibull 分布的竞争对手。

参考文献

[1]

[2]

Chhikara, Raj S., and Folks, J. Leroy, “The Inverse Gaussian Distribution: Theory : Methodology, and Applications”, CRC Press, 1988.

[3]

示例

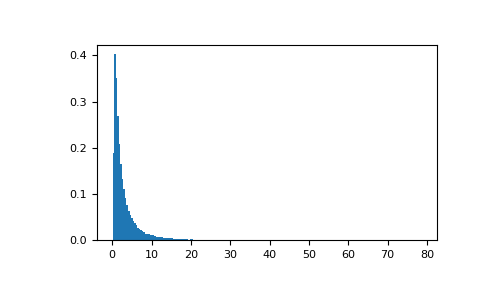
从分布中抽取值并绘制直方图

>>> import matplotlib.pyplot as plt
>>> h = plt.hist(np.random.wald(3, 2, 100000), bins=200, density=True)
>>> plt.show()