numpy.random.RandomState.logseries

方法

random.RandomState.logseries(p, size=None)

从对数级数分布中抽取样本。

从指定形状参数的 log series 分布中抽取样本，0 <= p < 1。

注意

新代码应该使用 logseries Generator 实例的方法；请参见 快速入门。

参数：

p浮点数或浮点数数组

分布的形状参数。必须在 [0, 1) 范围内。

size整数或整数元组，可选

输出形状。如果给定的形状例如为 (m, n, k)，则将抽取 m * n * k 个样本。如果 size 为 None（默认值），则如果 p 为标量，则返回单个值。否则，将抽取 np.array(p).size 个样本。

返回值：

outndarray 或标量

从参数化的对数级数分布中抽取的样本。

参见

scipy.stats.logser

概率密度函数、分布或累积密度函数等。

random.Generator.logseries

这应该用于新代码。

备注

对数级数分布的概率密度为

\[P(k) = \frac{-p^k}{k \ln(1-p)},\]

其中 p = 概率。

对数级数分布常用于表示物种丰富度和出现情况，首次由 Fisher、Corbet 和 Williams 于 1943 年提出 [2]。它也可用于模拟在汽车中看到的乘员人数 [3]。

参考文献

[1]

Buzas, Martin A.; Culver, Stephen J., Understanding regional species diversity through the log series distribution of occurrences: BIODIVERSITY RESEARCH Diversity & Distributions, Volume 5, Number 5, September 1999 , pp. 187-195(9).

[2]

Fisher, R.A,, A.S. Corbet, and C.B. Williams. 1943. The relation between the number of species and the number of individuals in a random sample of an animal population. Journal of Animal Ecology, 12:42-58.

[3]

D. J. Hand, F. Daly, D. Lunn, E. Ostrowski, A Handbook of Small Data Sets, CRC Press, 1994.

[4]

Wikipedia，“对数分布”，https://en.wikipedia.org/wiki/Logarithmic_distribution

示例

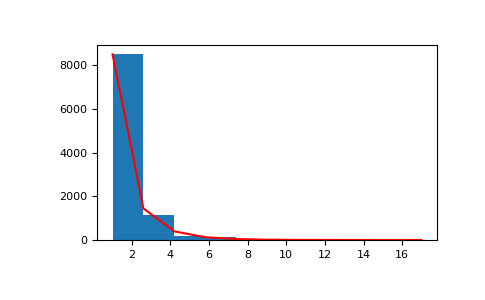
从分布中抽取样本

>>> a = .6
>>> s = np.random.logseries(a, 10000)
>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s)

# 对比分布作图

>>> def logseries(k, p):
...     return -p**k/(k*np.log(1-p))
>>> plt.plot(bins, logseries(bins, a)*count.max()/
...          logseries(bins, a).max(), 'r')
>>> plt.show()