numpy.random.standard_gamma#
- random.standard_gamma(shape, size=None)#
从标准 Gamma 分布中抽取样本。
样本是从具有指定参数(形状,有时表示为“k”)且尺度 scale=1 的 Gamma 分布中抽取的。
注意
新代码应改用
Generator实例的standard_gamma方法;请参阅 快速入门。- 参数:
- shape浮点数或浮点数数组
参数,必须是非负数。
- size整数或整数元组,可选
输出形状。例如,如果给定形状为
(m, n, k),则抽取m * n * k个样本。如果 size 为None(默认值),则当shape为标量时返回单个值。否则,抽取np.array(shape).size个样本。
- 返回:
- outndarray 或 标量
从参数化的标准 Gamma 分布中抽取的样本。
另请参阅
scipy.stats.gamma概率密度函数、分布或累积密度函数等。
random.Generator.standard_gamma新代码应使用此函数。
备注
Gamma 分布的概率密度函数为
\[p(x) = x^{k-1}\frac{e^{-x/\theta}}{\theta^k\Gamma(k)},\]其中 \(k\) 是形状参数,\(\theta\) 是尺度参数,\(\Gamma\) 是 Gamma 函数。
Gamma 分布常用于模拟电子元件的故障时间,并且自然出现在与泊松分布事件之间等待时间相关的过程中。
参考文献
[1]Weisstein, Eric W. “Gamma Distribution.” 来自 MathWorld–A Wolfram Web Resource。 https://mathworld.net.cn/GammaDistribution.html
[2]维基百科,“Gamma distribution”, https://en.wikipedia.org/wiki/Gamma_distribution
示例
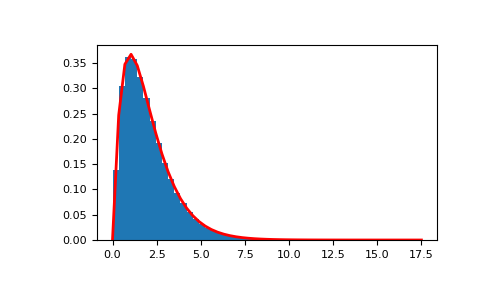
从分布中抽取样本
>>> shape, scale = 2., 1. # mean and width >>> s = np.random.standard_gamma(shape, 1000000)
显示样本的直方图以及概率密度函数
>>> import matplotlib.pyplot as plt >>> import scipy.special as sps >>> count, bins, ignored = plt.hist(s, 50, density=True) >>> y = bins**(shape-1) * ((np.exp(-bins/scale))/ ... (sps.gamma(shape) * scale**shape)) >>> plt.plot(bins, y, linewidth=2, color='r') >>> plt.show()