numpy.random.Generator.vonmises#
方法
- random.Generator.vonmises(mu, kappa, size=None)#
从 von Mises 分布中抽取样本。
从具有指定模式 (mu) 和集中度 (kappa) 的 von Mises 分布中抽取样本,在区间 [-pi, pi] 上。
von Mises 分布(也称为圆形正态分布)是单位圆上的连续概率分布。可以将其视为正态分布的圆形模拟。
- 参数:
- mu浮点数或浮点数数组
分布的模式(“中心”)。
- kappa浮点数或浮点数数组
分布的集中度,必须 >=0。
- size整数或整数元组,可选
输出形状。如果给定形状为例如
(m, n, k),则会抽取m * n * k个样本。如果 size 为None(默认值),则当mu和kappa均为标量时,返回单个值。否则,抽取np.broadcast(mu, kappa).size个样本。
- 返回:
- outndarray 或标量
从参数化的 von Mises 分布中抽取的样本。
另请参见
scipy.stats.vonmises概率密度函数、分布或累积密度函数等。
备注
von Mises 分布的概率密度为
\[p(x) = \frac{e^{\kappa cos(x-\mu)}}{2\pi I_0(\kappa)},\]其中 \(\mu\) 是模式,\(\kappa\) 是集中度,\(I_0(\kappa)\) 是 0 阶修正贝塞尔函数。
von Mises 以 Richard Edler von Mises 命名,他出生于奥匈帝国(现乌克兰)。他于 1939 年逃往美国,成为哈佛大学的教授。他从事概率论、空气动力学、流体力学和科学哲学领域的工作。
参考文献
[1]Abramowitz, M. and Stegun, I. A. (Eds.). “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing,” New York: Dover, 1972.
[2]von Mises, R., “Mathematical Theory of Probability and Statistics”, New York: Academic Press, 1964.
示例
从分布中抽取样本
>>> mu, kappa = 0.0, 4.0 # mean and concentration >>> rng = np.random.default_rng() >>> s = rng.vonmises(mu, kappa, 1000)
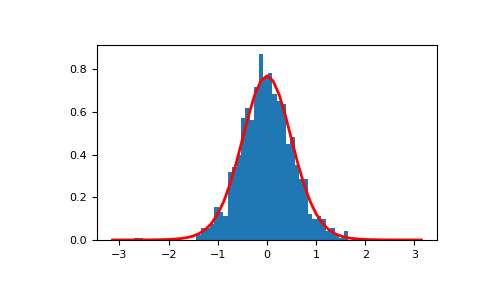
显示样本的直方图以及概率密度函数
>>> import matplotlib.pyplot as plt >>> from scipy.special import i0 >>> plt.hist(s, 50, density=True) >>> x = np.linspace(-np.pi, np.pi, num=51) >>> y = np.exp(kappa*np.cos(x-mu))/(2*np.pi*i0(kappa)) >>> plt.plot(x, y, linewidth=2, color='r') >>> plt.show()