numpy.random.multivariate_normal#
- random.multivariate_normal(mean, cov, size=None, check_valid='warn', tol=1e-8)#
从多元正态分布中抽取随机样本。
多元正态分布、多正态分布或高斯分布是一维正态分布向更高维度的推广。这种分布由其均值和协方差矩阵指定。这些参数类似于一维正态分布的均值(平均值或“中心”)和方差(标准差的平方或“宽度”的平方)。
注意
新代码应改用
Generator实例的multivariate_normal方法;请参阅快速入门。- 参数:
- mean1-D 数组,长度为 N
N 维分布的均值。
- cov2-D 数组,形状为 (N, N)
分布的协方差矩阵。它必须是对称的半正定矩阵,才能进行正确的抽样。
- sizeint 或 int 的元组,可选
例如,给定形状为
(m,n,k),则会生成m*n*k个样本,并以 m 行 n 列 k 深度的排列方式打包。由于每个样本是 N 维的,因此输出形状为(m,n,k,N)。如果未指定形状,则返回一个单(N 维)样本。- check_valid{ 'warn', 'raise', 'ignore' },可选
当协方差矩阵不是半正定时的行为。
- tol浮点数,可选
检查协方差矩阵中奇异值时的容差。在检查之前,cov 会被转换为双精度浮点数。
- 返回:
- outndarray
抽取的样本,如果提供了 size,则形状为 size。否则,形状为
(N,)。换句话说,每个条目
out[i,j,...,:]都是从该分布中抽取的一个 N 维值。
另请参阅
random.Generator.multivariate_normal新代码应使用此方法。
注意
均值是 N 维空间中的一个坐标,表示最有可能生成样本的位置。这类似于一维或单变量正态分布的钟形曲线的峰值。
协方差表示两个变量一起变化的程度。从多元正态分布中,我们抽取 N 维样本,\(X = [x_1, x_2, ... x_N]\)。协方差矩阵元素 \(C_{ij}\) 是 \(x_i\) 和 \(x_j\) 的协方差。元素 \(C_{ii}\) 是 \(x_i\) 的方差(即其“离散程度”)。
除了指定完整的协方差矩阵,常见的近似包括:
通过绘制生成的数据点,可以在二维空间中看到这种几何特性
>>> mean = [0, 0] >>> cov = [[1, 0], [0, 100]] # diagonal covariance
对角协方差意味着点沿 x 轴或 y 轴方向排列
>>> import matplotlib.pyplot as plt >>> x, y = np.random.multivariate_normal(mean, cov, 5000).T >>> plt.plot(x, y, 'x') >>> plt.axis('equal') >>> plt.show()
请注意,协方差矩阵必须是半正定(即非负定)的。否则,此方法的行为是未定义的,并且不保证向后兼容性。
参考
[1]Papoulis, A., “概率、随机变量和随机过程”,第3版,纽约:McGraw-Hill,1991年。
[2]Duda, R. O., Hart, P. E., 和 Stork, D. G., “模式分类”,第2版,纽约:Wiley,2001年。
示例
>>> mean = (1, 2) >>> cov = [[1, 0], [0, 1]] >>> x = np.random.multivariate_normal(mean, cov, (3, 3)) >>> x.shape (3, 3, 2)
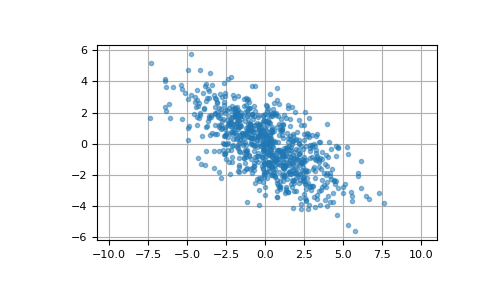
这里我们从均值为 [0, 0]、协方差矩阵为 [[6, -3], [-3, 3.5]] 的二元正态分布中生成 800 个样本。样本的第一个和第二个分量的预期方差分别为 6 和 3.5,预期相关系数为 -3/sqrt(6*3.5) ≈ -0.65465。
>>> cov = np.array([[6, -3], [-3, 3.5]]) >>> pts = np.random.multivariate_normal([0, 0], cov, size=800)
检查样本的均值、协方差和相关系数是否接近预期值
>>> pts.mean(axis=0) array([ 0.0326911 , -0.01280782]) # may vary >>> np.cov(pts.T) array([[ 5.96202397, -2.85602287], [-2.85602287, 3.47613949]]) # may vary >>> np.corrcoef(pts.T)[0, 1] -0.6273591314603949 # may vary
我们可以用散点图来可视化这些数据。点云的方向说明了该样本分量之间的负相关性。
>>> import matplotlib.pyplot as plt >>> plt.plot(pts[:, 0], pts[:, 1], '.', alpha=0.5) >>> plt.axis('equal') >>> plt.grid() >>> plt.show()