numpy.random.lognormal

random.lognormal(mean=0.0, sigma=1.0, size=None)

从对数正态分布中抽取样本。

从指定均值、标准差和数组形状的对数正态分布中抽取样本。注意，这里的均值和标准差并非分布本身的均值和标准差，而是其所派生的底层正态分布的均值和标准差。

注意

新代码应该使用 Generator 实例的 lognormal 方法；请参阅 快速入门。

参数:

meanfloat 或 float 的 array_like，可选

底层正态分布的均值。默认为 0。

sigmafloat 或 float 的 array_like，可选

底层正态分布的标准差。必须是非负数。默认为 1。

sizeint 或 int 的 tuple，可选

输出形状。如果给定的形状是例如 (m, n, k)，则抽取 m * n * k 个样本。如果 size 是 None (默认)，并且 mean 和 sigma 都是标量，则返回一个单一值。否则，抽取 np.broadcast(mean, sigma).size 个样本。

返回:

outndarray 或 scalar

从参数化对数正态分布中抽取的样本。

另请参阅

scipy.stats.lognorm

概率密度函数、分布、累积密度函数等。

random.Generator.lognormal

新代码应该使用此方法。

注意事项

如果 log(x) 服从正态分布，则变量 x 服从对数正态分布。对数正态分布的概率密度函数为

\[p(x) = \frac{1}{\sigma x \sqrt{2\pi}} e^{(-\frac{(ln(x)-\mu)^2}{2\sigma^2})}\]

其中 \(\mu\) 是该变量的服从正态分布的对数的均值，\(\sigma\) 是其标准差。当一个随机变量是大量独立的、同分布的变量的乘积时，会得到对数正态分布；这与当变量是大量独立的、同分布的变量的总和时得到正态分布的方式相同。

参考文献

[1]

Limpert, E., Stahel, W. A., and Abbt, M., “Log-normal Distributions across the Sciences: Keys and Clues,” BioScience, Vol. 51, No. 5, May, 2001. https://stat.ethz.ch/~stahel/lognormal/bioscience.pdf

[2]

Reiss, R.D. and Thomas, M., “Statistical Analysis of Extreme Values,” Basel: Birkhauser Verlag, 2001, pp. 31-32.

示例

在浏览器中试试！

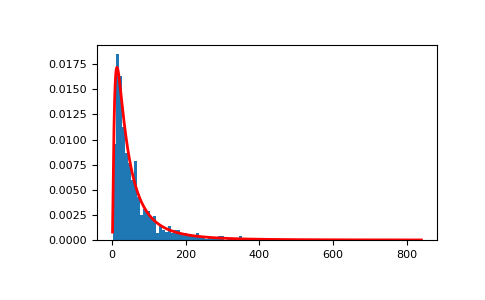
从分布中抽取样本

>>> mu, sigma = 3., 1. # mean and standard deviation
>>> s = np.random.lognormal(mu, sigma, 1000)

显示样本的直方图以及概率密度函数

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 100, density=True, align='mid')

>>> x = np.linspace(min(bins), max(bins), 10000)
>>> pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * np.sqrt(2 * np.pi)))

>>> plt.plot(x, pdf, linewidth=2, color='r')
>>> plt.axis('tight')
>>> plt.show()

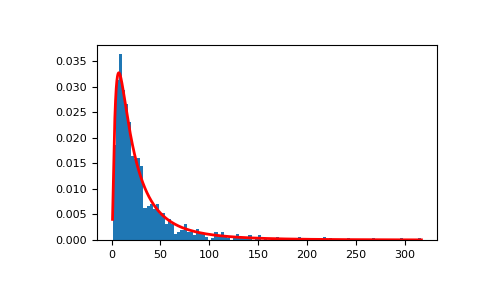
演示对来自均匀分布的随机样本进行乘积运算后，其结果可以很好地拟合对数正态概率密度函数。

>>> # Generate a thousand samples: each is the product of 100 random
>>> # values, drawn from a normal distribution.
>>> b = []
>>> for i in range(1000):
...    a = 10. + np.random.standard_normal(100)
...    b.append(np.prod(a))

>>> b = np.array(b) / np.min(b) # scale values to be positive
>>> count, bins, ignored = plt.hist(b, 100, density=True, align='mid')
>>> sigma = np.std(np.log(b))
>>> mu = np.mean(np.log(b))

>>> x = np.linspace(min(bins), max(bins), 10000)
>>> pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * np.sqrt(2 * np.pi)))

>>> plt.plot(x, pdf, color='r', linewidth=2)
>>> plt.show()

返回在新标签页中打开