numpy.unwrap#

numpy.unwrap(p, discont=None, axis=-1, *, period=6.283185307179586)[源代码]#

通过相对于周期取大增量的补数来展开。

这会通过将与前一个元素之间的绝对差大于 max(discont, period/2) 的元素更改为它们的 period 补数来展开信号 p。

对于默认情况，其中 period 是 \(2\pi\) 且 discont 是 \(\pi\)，这会展开一个弧度相位 p，使得相邻差值从不大于 \(\pi\)，通过加上 \(2k\pi\)（其中 \(k\) 是某个整数）。

参数:

parray_like: 输入数组。
discontfloat, optional: 值之间的最大不连续性，默认为 period/2。低于 period/2 的值将被视为 period/2。要产生与默认值不同的效果，discont 应大于 period/2。
axisint, optional: 展开操作将沿轴执行，默认为最后一个轴。
periodfloat, optional: 输入信号的缠绕范围大小。默认值为 2 pi。

版本 1.21.0 中新增。

返回:

outndarray: 输出数组。

另请参阅

rad2deg, deg2rad

备注

如果 p 中的不连续性小于 period/2，但大于 discont，则不执行展开，因为取补数只会使不连续性更大。

示例

>>> import numpy as np

>>> phase = np.linspace(0, np.pi, num=5)
>>> phase[3:] += np.pi
>>> phase
array([ 0.        ,  0.78539816,  1.57079633,  5.49778714,  6.28318531]) # may vary
>>> np.unwrap(phase)
array([ 0.        ,  0.78539816,  1.57079633, -0.78539816,  0.        ]) # may vary
>>> np.unwrap([0, 1, 2, -1, 0], period=4)
array([0, 1, 2, 3, 4])
>>> np.unwrap([ 1, 2, 3, 4, 5, 6, 1, 2, 3], period=6)
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> np.unwrap([2, 3, 4, 5, 2, 3, 4, 5], period=4)
array([2, 3, 4, 5, 6, 7, 8, 9])
>>> phase_deg = np.mod(np.linspace(0 ,720, 19), 360) - 180
>>> np.unwrap(phase_deg, period=360)
array([-180., -140., -100.,  -60.,  -20.,   20.,   60.,  100.,  140.,
        180.,  220.,  260.,  300.,  340.,  380.,  420.,  460.,  500.,
        540.])

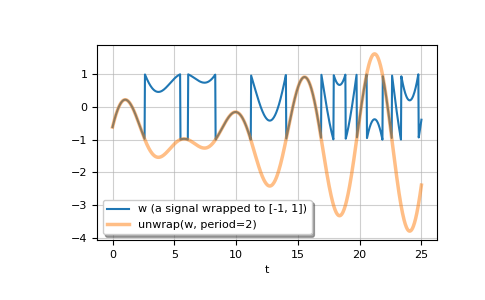
此示例绘制了缠绕输入信号 w 的展开过程。首先生成 w，然后应用 unwrap 得到 u。

>>> t = np.linspace(0, 25, 801)
>>> w = np.mod(1.5 * np.sin(1.1 * t + 0.26) * (1 - t / 6 + (t / 23) ** 3), 2.0) - 1
>>> u = np.unwrap(w, period=2.0)

绘制 w 和 u。

>>> import matplotlib.pyplot as plt
>>> plt.plot(t, w, label='w (a signal wrapped to [-1, 1])')
>>> plt.plot(t, u, linewidth=2.5, alpha=0.5, label='unwrap(w, period=2)')
>>> plt.xlabel('t')
>>> plt.grid(alpha=0.6)
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.show()