numpy.linalg.lstsq#

linalg.lstsq(a, b, rcond=None)[源码]#

返回线性矩阵方程的最小二乘解。

计算向量 x，使其近似解方程 a @ x = b。该方程可能是欠定、恰定或超定的（即 a 的线性无关行数可以小于、等于或大于其线性无关列数）。如果 a 是方阵且满秩，则 x （除舍入误差外）是方程的“精确”解。否则，x 使欧几里得 2-范数 \(||b - ax||\) 最小化。如果存在多个最小化解，则返回 2-范数 \(||x||\) 最小的那个。

参数:

a(M, N) array_like: “系数”矩阵。
b{(M,), (M, K)} array_like: 纵坐标或“因变量”值。如果 b 是二维的，则对 b 的每个 K 列计算最小二乘解。
rcondfloat, optional: 用于 a 的小奇异值的截断比率。为了确定秩，如果奇异值小于 rcond 乘以 a 的最大奇异值，则将其视为零。默认值使用机器精度乘以 max(M, N)。传入 -1 将使用机器精度。

2.0 版本中更改: 此前，默认值为 -1，但已发出警告称此值将发生变化。

返回:

x{(N,), (N, K)} ndarray: 最小二乘解。如果 b 是二维的，则解位于 x 的 K 列中。
residuals{(1,), (K,), (0,)} ndarray: 残差平方和：b - a @ x 中每列的欧几里得 2-范数平方。如果 a 的秩小于 N 或 M <= N，则这是一个空数组。如果 b 是一维的，则这是一个 (1,) 形状的数组。否则形状为 (K,)。
rankint: 矩阵 a 的秩。
s(min(M, N),) ndarray: a 的奇异值。

引发:

LinAlgError: 如果计算不收敛。

另请参阅

scipy.linalg.lstsq: SciPy 中类似的函数。

注意

如果 b 是一个矩阵，则所有数组结果都作为矩阵返回。

示例

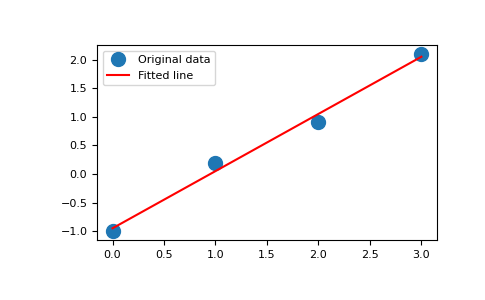
通过一些嘈杂的数据点拟合一条直线 y = mx + c

>>> import numpy as np
>>> x = np.array([0, 1, 2, 3])
>>> y = np.array([-1, 0.2, 0.9, 2.1])

通过检查系数，我们看到这条直线的斜率大约为 1，并且大致在 -1 处与 y 轴相交。

我们可以将直线方程改写为 y = Ap，其中 A = [[x 1]] 且 p = [[m], [c]]。现在使用 lstsq 求解 p。

>>> A = np.vstack([x, np.ones(len(x))]).T
>>> A
array([[ 0.,  1.],
       [ 1.,  1.],
       [ 2.,  1.],
       [ 3.,  1.]])

>>> m, c = np.linalg.lstsq(A, y)[0]
>>> m, c
(1.0 -0.95) # may vary

绘制数据和拟合线

>>> import matplotlib.pyplot as plt
>>> _ = plt.plot(x, y, 'o', label='Original data', markersize=10)
>>> _ = plt.plot(x, m*x + c, 'r', label='Fitted line')
>>> _ = plt.legend()
>>> plt.show()