numpy.random.triangular#
- random.triangular(left, mode, right, size=None)#
从区间
[left, right]上的三角形分布中抽取样本。三角分布是一种连续概率分布,下限为 `left`,峰值在 `mode`,上限为 `right`。与其他分布不同,这些参数直接定义了概率密度函数(pdf)的形状。
注意
新代码应使用
triangular方法,而不是Generator实例;请参阅 快速入门。- 参数:
- leftfloat 或 array_like of floats
下限。
- modefloat 或 array_like of floats
分布峰值出现的数值。该值必须满足条件
left <= mode <= right。- rightfloat 或 array_like of floats
上限,必须大于 `left`。
- sizeint 或 int 的元组,可选
输出形状。如果给定的形状例如是
(m, n, k),则将抽取m * n * k个样本。如果 `size` 是None(默认值),并且 `left`、`mode` 和 `right` 都是标量,则返回单个值。否则,将抽取np.broadcast(left, mode, right).size个样本。
- 返回:
- outndarray 或标量
从参数化的三角分布中抽取样本。
另请参阅
random.Generator.triangular新代码应使用此方法。
备注
三角分布的概率密度函数为
\[\begin{split}P(x;l, m, r) = \begin{cases} \frac{2(x-l)}{(r-l)(m-l)}& \text{当 $l \leq x \leq m$ 时},\\ \frac{2(r-x)}{(r-l)(r-m)}& \text{当 $m \leq x \leq r$ 时},\\ 0& \text{其他情况}. \end{cases}\end{split}\]三角分布常用于定义不明确的问题,在这种问题中,基础分布未知,但对边界和峰值有一些了解。它经常用于模拟中。
参考
[1]维基百科,“Triangular distribution” https://en.wikipedia.org/wiki/Triangular_distribution
示例
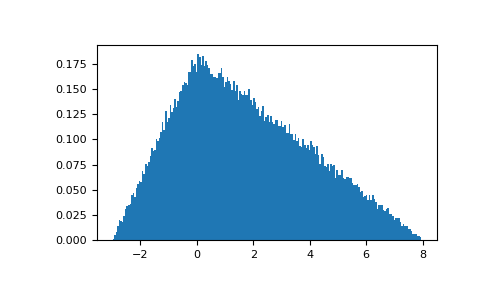
从分布中抽取数值并绘制直方图
>>> import matplotlib.pyplot as plt >>> h = plt.hist(np.random.triangular(-3, 0, 8, 100000), bins=200, ... density=True) >>> plt.show()