numpy.random.poisson#

random.poisson(lam=1.0, size=None)#

从泊松分布中抽取样本。

泊松分布是二项分布在 N 很大的极限情况。

注意

新代码应使用 Generator 实例的 poisson 方法；请参阅 快速入门。

参数:
lamfloat 或 float 的 array_like

在固定时间间隔内发生的事件的期望数量，必须大于或等于 0。序列必须可广播到请求的大小。

sizeint 或 int 的元组，可选

输出形状。如果给定的形状是，例如，(m, n, k)，那么将抽取 m * n * k 个样本。如果 size 是 None（默认），当 lam 是标量时，将返回单个值。否则，将抽取 np.array(lam).size 个样本。

返回:
outndarray 或标量

从参数化的泊松分布中抽取的样本。

另请参阅

random.Generator.poisson

新代码应使用此方法。

备注

泊松分布的概率质量函数（PMF）是

\[f(k; \lambda)=\frac{\lambda^k e^{-\lambda}}{k!}\]

对于期望间隔为 \(\lambda\) 的事件，泊松分布 \(f(k; \lambda)\) 描述了在观测间隔 \(\lambda\) 内发生 \(k\) 个事件的概率。

由于输出被限制在 C int64 类型范围内，当 lam 接近最大可表示值 10 个标准差以内时，会引发 ValueError。

参考

[1]

Weisstein, Eric W. “Poisson Distribution.” From MathWorld–A Wolfram Web Resource. https://mathworld.net.cn/PoissonDistribution.html

[2]

Wikipedia, “Poisson distribution”, https://en.wikipedia.org/wiki/Poisson_distribution

示例

从分布中绘制样本

>>> import numpy as np
>>> s = np.random.poisson(5, 10000)

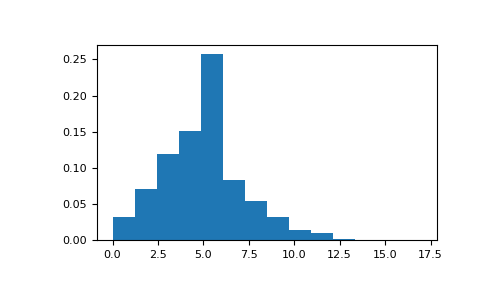
显示样本的直方图

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 14, density=True)
>>> plt.show()
../../../_images/numpy-random-poisson-1_00_00.png

为 lambda 100 和 500 分别抽取 100 个值

>>> s = np.random.poisson(lam=(100., 500.), size=(100, 2))
在此页面