numpy.random.laplace#

random.laplace(loc=0.0, scale=1.0, size=None)#

从具有指定位置（或均值）和尺度（衰减）的 Laplace 或双指数分布中抽取样本。

拉普拉斯分布类似于高斯/正态分布，但在峰值处更尖锐，尾部更肥胖。它表示两个独立同分布的指数随机变量之差。

注意

新代码应使用 Generator 实例的 laplace 方法；请参阅快速入门。

参数:

locfloat 或 array_like of floats, optional: 分布峰值的位置，\(\mu\)。默认为 0。
scalefloat 或 array_like of floats, optional: \(\lambda\)，指数衰减。默认为 1。必须是非负的。
sizeint 或 int 的元组，可选: 输出形状。如果给定的形状是，例如，(m, n, k)，则绘制 m * n * k 个样本。如果 size 为 None（默认），则当 loc 和 scale 均为标量时，将返回单个值。否则，将绘制 np.broadcast(loc, scale).size 个样本。

返回:

outndarray 或标量: 从参数化拉普拉斯分布中抽取样本。

另请参阅

random.Generator.laplace: 新代码应使用此方法。

备注

它的概率密度函数为

\[f(x; \mu, \lambda) = \frac{1}{2\lambda} \exp\left(-\frac{|x - \mu|}{\lambda}\right).\]

拉普拉斯的第一定律，发表于1774年，指出误差的频率可以表示为误差绝对幅度的指数函数，这导致了拉普拉斯分布。对于经济学和健康科学中的许多问题，这种分布似乎比标准高斯分布更能很好地拟合数据。

参考

[1]

Abramowitz, M. and Stegun, I. A. (Eds.). “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing,” New York: Dover, 1972.

[2]

Kotz, Samuel, et. al. “The Laplace Distribution and Generalizations, “ Birkhauser, 2001.

[3]

Weisstein, Eric W. “Laplace Distribution.” From MathWorld–A Wolfram Web Resource. https://mathworld.net.cn/LaplaceDistribution.html

[4]

Wikipedia, “Laplace distribution”, https://en.wikipedia.org/wiki/Laplace_distribution

示例

从分布中绘制样本

>>> loc, scale = 0., 1.
>>> s = np.random.laplace(loc, scale, 1000)

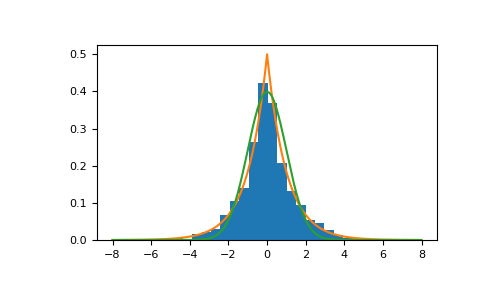
显示样本的直方图以及概率密度函数

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 30, density=True)
>>> x = np.arange(-8., 8., .01)
>>> pdf = np.exp(-abs(x-loc)/scale)/(2.*scale)
>>> plt.plot(x, pdf)

绘制高斯分布以进行比较

>>> g = (1/(scale * np.sqrt(2 * np.pi)) *
...      np.exp(-(x - loc)**2 / (2 * scale**2)))
>>> plt.plot(x,g)

../../../_images/numpy-random-laplace-1.png