numpy.random.Generator.geometric#
方法
- random.Generator.geometric(p, size=None)#
从几何分布中抽取样本。
伯努利试验是具有两种结果之一的实验:成功或失败(抛硬币就是这样的实验)。几何分布模拟了实现成功所需的试验次数。因此,它定义在正整数
k = 1, 2, ...上。几何分布的概率质量函数是
\[f(k) = (1 - p)^{k - 1} p\]其中 p 是单次试验成功的概率。
- 参数:
- p浮点数或类数组的浮点数
单次试验成功的概率。
- sizeint 或 int 的元组,可选
输出形状。如果给定的形状是,例如,
(m, n, k),则抽取m * n * k个样本。如果 size 为None(默认),当p为标量时,将返回单个值。否则,将抽取np.array(p).size个样本。
- 返回:
- outndarray 或标量
从参数化的几何分布中绘制样本。
参考
[1]维基百科,“几何分布”,https://en.wikipedia.org/wiki/Geometric_distribution
示例
从几何分布中抽取 10,000 个值,单次成功的概率为
p = 0.35>>> p, size = 0.35, 10000 >>> rng = np.random.default_rng() >>> sample = rng.geometric(p=p, size=size)
单次运行后成功的试验比例是多少?
>>> (sample == 1).sum()/size 0.34889999999999999 # may vary
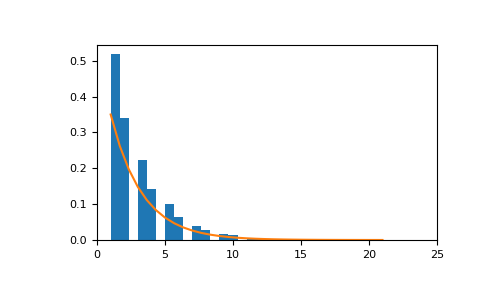
参数为
p=0.35的几何分布如下所示>>> import matplotlib.pyplot as plt >>> count, bins, _ = plt.hist(sample, bins=30, density=True) >>> plt.plot(bins, (1-p)**(bins-1)*p) >>> plt.xlim([0, 25]) >>> plt.show()