numpy.random.Generator.f#
方法
- random.Generator.f(dfnum, dfden, size=None)#
从 F 分布中抽取样本。
从具有指定参数 dfnum(分子自由度)和 dfden(分母自由度)的 F 分布中抽取样本,这两个参数都必须大于零。
F 分布(也称为 Fisher 分布)的随机变量是一种连续概率分布,出现在 ANOVA 检验中,是两个卡方变量的比率。
- 参数:
- dfnum浮点数或浮点数数组类型
分子自由度,必须 > 0。
- dfden浮点数或浮点数数组类型
分母自由度,必须 > 0。
- sizeint 或 int 元组,可选
输出形状。如果给定形状为例如
(m, n, k),则抽取m * n * k个样本。如果 size 为None(默认值),则当dfnum和dfden都是标量时,返回单个值。否则,抽取np.broadcast(dfnum, dfden).size个样本。
- 返回:
- outndarray 或标量
从参数化的 Fisher 分布中抽取的样本。
另请参阅
scipy.stats.f概率密度函数、分布或累积密度函数等。
注释
F 统计量用于比较组内方差与组间方差。分布的计算取决于抽样,因此它是问题中各个自由度的函数。变量 dfnum 是样本数减一,即组间自由度,而 dfden 是组内自由度,即每组样本数之和减去组数。
参考文献
[1]Glantz, Stanton A. “生物统计学入门。”,McGraw-Hill,第五版,2002。
[2]维基百科,“F-分布”,https://en.wikipedia.org/wiki/F-distribution
示例
Glantz[1] 中的一个示例,第 47-40 页
两组,糖尿病患者的子女(25人)和非糖尿病患者的子女(25名对照)。测量空腹血糖,病例组平均值为 86.1,对照组平均值为 82.2。标准差分别为 2.09 和 2.49。这些数据是否与“父母的糖尿病状况不影响其子女血糖水平”的零假设一致?从数据中计算 F 统计量得到的值为 36.01。
从分布中抽取样本
>>> dfnum = 1. # between group degrees of freedom >>> dfden = 48. # within groups degrees of freedom >>> rng = np.random.default_rng() >>> s = rng.f(dfnum, dfden, 1000)
样本前 1% 的下限是
>>> np.sort(s)[-10] 7.61988120985 # random
因此 F 统计量超过 7.62 的概率约为 1%,测量值为 36,因此在 1% 的显著性水平上拒绝零假设。
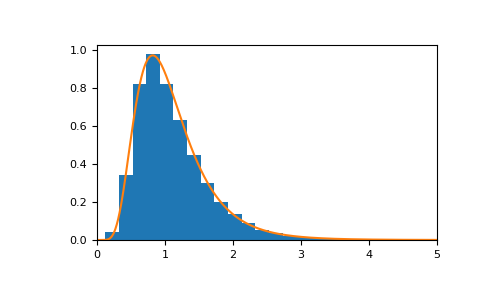
当
n = 20且m = 20时,对应的概率密度函数是>>> import matplotlib.pyplot as plt >>> from scipy import stats >>> dfnum, dfden, size = 20, 20, 10000 >>> s = rng.f(dfnum=dfnum, dfden=dfden, size=size) >>> bins, density, _ = plt.hist(s, 30, density=True) >>> x = np.linspace(0, 5, 1000) >>> plt.plot(x, stats.f.pdf(x, dfnum, dfden)) >>> plt.xlim([0, 5]) >>> plt.show()