numpy.random.Generator.chisquare#

方法

random.Generator.chisquare(df, size=None)#

从卡方分布中抽取样本。

当 df 个独立的、服从标准正态分布（均值 0，方差 1）的随机变量进行平方和求和时，所得的分布即为卡方分布（参见“注意”）。此分布常用于假设检验。

参数:

df浮点数或浮点数数组: 自由度，必须大于 0。
size整数或整数元组，可选: 输出形状。如果给定形状为，例如 (m, n, k)，则抽取 m * n * k 个样本。如果 size 为 None（默认值），当 df 为标量时，将返回单个值。否则，将抽取 np.array(df).size 个样本。

返回:

outndarray 或标量: 从参数化的卡方分布中抽取的样本。

抛出:

ValueError: 当 df <= 0 或给定不合适的 size（例如 size=-1）时。

注意

通过对 df 个独立的、服从标准正态分布的随机变量的平方求和而获得的变量

\[Q = \sum_{i=1}^{\mathtt{df}} X^2_i\]

服从卡方分布，表示为

\[Q \sim \chi^2_k.\]

卡方分布的概率密度函数为

\[p(x) = \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2},\]

其中 \(\Gamma\) 是伽马函数，

\[\Gamma(x) = \int_0^{-\infty} t^{x - 1} e^{-t} dt.\]

参考文献

[1]

NIST “工程统计手册” https://www.itl.nist.gov/div898/handbook/eda/section3/eda3666.htm

示例

>>> rng = np.random.default_rng()
>>> rng.chisquare(2,4)
array([ 1.89920014,  9.00867716,  3.13710533,  5.62318272]) # random

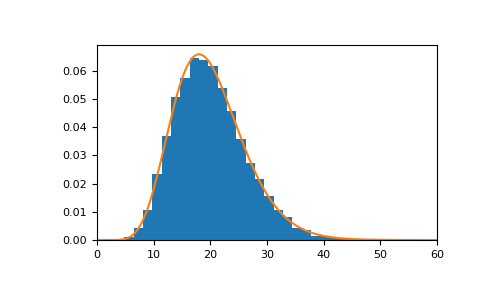
具有 20 个自由度的卡方随机变量的分布如下所示

>>> import matplotlib.pyplot as plt
>>> import scipy.stats as stats
>>> s = rng.chisquare(20, 10000)
>>> count, bins, _ = plt.hist(s, 30, density=True)
>>> x = np.linspace(0, 60, 1000)
>>> plt.plot(x, stats.chi2.pdf(x, df=20))
>>> plt.xlim([0, 60])
>>> plt.show()

../../../_images/numpy-random-Generator-chisquare-1.png