numpy.fft.fft

fft.fft(a, n=None, axis=-1, norm=None, out=None)

计算一维离散傅里叶变换。

此函数使用高效的快速傅里叶变换 (FFT) 算法 [CT] 计算一维 *n* 点离散傅里叶变换 (DFT)。

参数：

aarray_like

输入数组，可以是复数。

nint, optional

输出变换轴的长度。如果 *n* 小于输入长度，则裁剪输入。如果大于输入长度，则用零填充输入。如果未给出 *n*，则使用由 *axis* 指定的轴上的输入长度。

axisint, optional

计算 FFT 的轴。如果未给出，则使用最后一个轴。

norm{“backward”, “ortho”, “forward”}, optional

归一化模式（参见 numpy.fft）。默认为“backward”。指示正向/反向变换对中的哪个方向进行缩放以及使用什么归一化因子。

版本 1.20.0 中的新功能： 添加了“backward”、“forward”值。

outcomplex ndarray, optional

如果提供，结果将放置在此数组中。它应该具有适当的形状和数据类型。

版本 2.0.0 中的新功能。

返回：

outcomplex ndarray

沿由 *axis* 指示的轴（如果未指定 *axis* 则为最后一个轴）变换的截断或零填充输入。

引发：

IndexError

如果 *axis* 不是 *a* 的有效轴。

另请参见

numpy.fft

有关 DFT 的定义和使用的约定。

ifft

fft 的逆变换。

fft2

二维 FFT。

fftn

*n* 维 FFT。

rfftn

实数输入的 *n* 维 FFT。

fftfreq

给定 FFT 参数的频率箱。

备注

FFT（快速傅里叶变换）指的是通过利用计算项中的对称性来高效计算离散傅里叶变换 (DFT) 的一种方法。当 *n* 为 2 的幂时，对称性最高，因此对于这些大小，变换效率最高。

DFT 的定义以及在此实现中使用的约定，在 numpy.fft 模块的文档中进行了描述。

参考文献

[CT]

Cooley, James W., and John W. Tukey, 1965, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19: 297-301.

示例

>>> import numpy as np
>>> np.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([-2.33486982e-16+1.14423775e-17j,  8.00000000e+00-1.25557246e-15j,
        2.33486982e-16+2.33486982e-16j,  0.00000000e+00+1.22464680e-16j,
       -1.14423775e-17+2.33486982e-16j,  0.00000000e+00+5.20784380e-16j,
        1.14423775e-17+1.14423775e-17j,  0.00000000e+00+1.22464680e-16j])

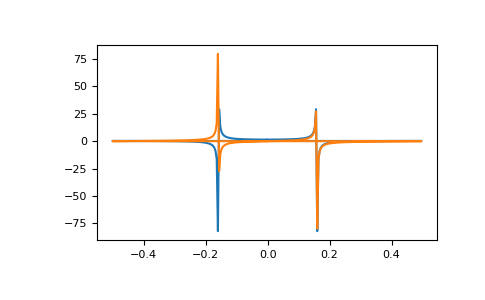
在此示例中，实数输入的 FFT 是厄米特矩阵，即实部对称，虚部反对称，如 numpy.fft 文档中所述。

>>> import matplotlib.pyplot as plt
>>> t = np.arange(256)
>>> sp = np.fft.fft(np.sin(t))
>>> freq = np.fft.fftfreq(t.shape[-1])
>>> plt.plot(freq, sp.real, freq, sp.imag)
[<matplotlib.lines.Line2D object at 0x...>, <matplotlib.lines.Line2D object at 0x...>]
>>> plt.show()