numpy.hamming#

numpy.hamming(M)[源代码]#

返回汉明窗。

汉明窗是一种通过加权余弦形成的衰减函数。

参数:

Mint: 输出窗口中的点数。如果为零或负数，则返回空数组。

返回:

outndarray: 窗口，其最大值归一化为一（当样本数量为奇数时，值一才会出现）。

另请参阅

bartlett, blackman, hanning, kaiser

备注

汉明窗定义为

\[w(n) = 0.54 - 0.46\cos\left(\frac{2\pi{n}}{M-1}\right) \qquad 0 \leq n \leq M-1\]

汉明窗以 R. W. Hamming 的名字命名，他是 J. W. Tukey 的同事，并在 Blackman 和 Tukey 的著作中有描述。它被推荐用于平滑时域中截断的自协方差函数。大多数关于汉明窗的引用都来自信号处理文献，其中它被用作众多平滑值的窗函数之一。它也称为“旁瓣衰减”（apodization）（意思是“去除脚”，即平滑采样信号开头和结尾处的间断）或锥度函数。

参考

[1]

Blackman, R.B. and Tukey, J.W., (1958) The measurement of power spectra, Dover Publications, New York.

[2]

E.R. Kanasewich，“Time Sequence Analysis in Geophysics”，The University of Alberta Press，1975 年，第 109-110 页。

[3]

维基百科，“窗口函数”，https://en.wikipedia.org/wiki/Window_function

[4]

W.H. Press，B.P. Flannery，S.A. Teukolsky 和 W.T. Vetterling，“Numerical Recipes”，Cambridge University Press，1986 年，第 425 页。

示例

>>> import numpy as np
>>> np.hamming(12)
array([ 0.08      ,  0.15302337,  0.34890909,  0.60546483,  0.84123594, # may vary
        0.98136677,  0.98136677,  0.84123594,  0.60546483,  0.34890909,
        0.15302337,  0.08      ])

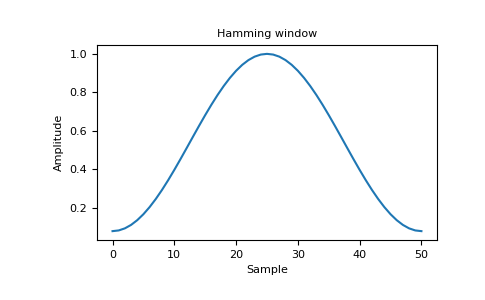
绘制窗口和频率响应。

import matplotlib.pyplot as plt
from numpy.fft import fft, fftshift
window = np.hamming(51)
plt.plot(window)
plt.title("Hamming window")
plt.ylabel("Amplitude")
plt.xlabel("Sample")
plt.show()

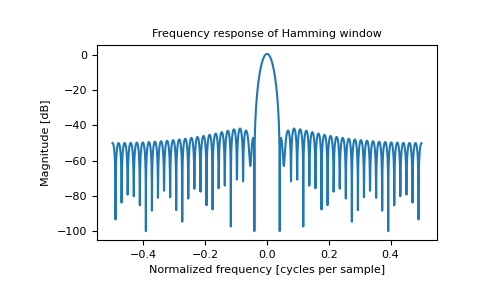
plt.figure()
A = fft(window, 2048) / 25.5
mag = np.abs(fftshift(A))
freq = np.linspace(-0.5, 0.5, len(A))
response = 20 * np.log10(mag)
response = np.clip(response, -100, 100)
plt.plot(freq, response)
plt.title("Frequency response of Hamming window")
plt.ylabel("Magnitude [dB]")
plt.xlabel("Normalized frequency [cycles per sample]")
plt.axis('tight')
plt.show()