numpy.blackman

numpy.blackman(M)

返回 Blackman 窗。

Blackman 窗是一个通过使用余弦函数求和的前三个项形成的锥形。它被设计成具有尽可能小的泄漏。它接近最优，仅略逊于 Kaiser 窗。

参数:

Mint

输出窗口中的点数。如果为零或更小，则返回一个空数组。

返回值:

outndarray

窗口，最大值归一化为 1（只有当样本数为奇数时，值 1 才出现）。

参见

bartlett，hamming，hanning，kaiser

注释

Blackman 窗定义为

\[w(n) = 0.42 - 0.5 \cos(2\pi n/M) + 0.08 \cos(4\pi n/M)\]

大多数关于 Blackman 窗的参考文献来自信号处理文献，其中它被用作平滑值的众多窗函数之一。它也被称为渐隐（意思是“去除底部”，即平滑采样信号开始和结束处的间断）或锥形函数。它被称为“近似最优”的锥形函数，几乎与 Kaiser 窗一样好（根据某些衡量标准）。

参考文献

Blackman, R.B. 和 Tukey, J.W.，(1958) 功率谱的测量，Dover 出版社，纽约。

Oppenheim, A.V. 和 R.W. Schafer。离散时间信号处理。新泽西州上萨德尔河：普伦蒂斯-霍尔，1999 年，第 468-471 页。

示例

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> np.blackman(12)
array([-1.38777878e-17,   3.26064346e-02,   1.59903635e-01, # may vary
        4.14397981e-01,   7.36045180e-01,   9.67046769e-01,
        9.67046769e-01,   7.36045180e-01,   4.14397981e-01,
        1.59903635e-01,   3.26064346e-02,  -1.38777878e-17])

绘制窗口和频率响应。

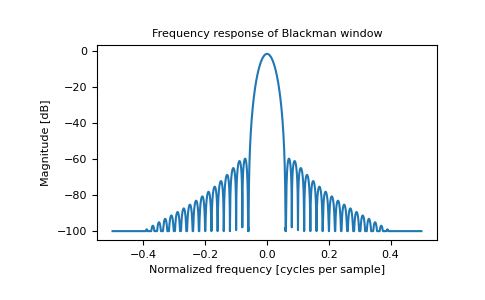
import matplotlib.pyplot as plt
from numpy.fft import fft, fftshift
window = np.blackman(51)
plt.plot(window)
plt.title("Blackman window")
plt.ylabel("Amplitude")
plt.xlabel("Sample")
plt.show()  # doctest: +SKIP

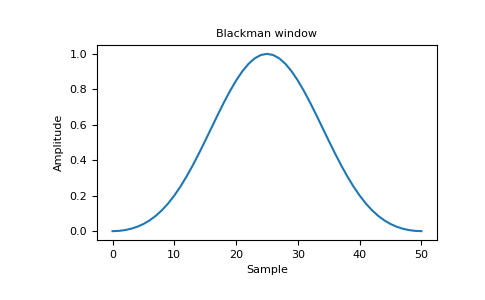
plt.figure()
A = fft(window, 2048) / 25.5
mag = np.abs(fftshift(A))
freq = np.linspace(-0.5, 0.5, len(A))
with np.errstate(divide='ignore', invalid='ignore'):
    response = 20 * np.log10(mag)
response = np.clip(response, -100, 100)
plt.plot(freq, response)
plt.title("Frequency response of Blackman window")
plt.ylabel("Magnitude [dB]")
plt.xlabel("Normalized frequency [cycles per sample]")
plt.axis('tight')
plt.show()