使用便利类#
多项式包提供的便利类包括:
在此上下文中,这些级数是相应多项式基函数乘以系数的有限和。例如,一个幂级数如下所示:
且系数为 \([1, 2, 3]\)。具有相同系数的切比雪夫级数如下所示:
更一般地,
其中在本例中,\(T_n\) 是 \(n\) 阶切比雪夫函数,但也可以是其他任何类的基函数。所有类的约定是系数 \(c[i]\) 对应 i 阶基函数。
所有类都是不可变的,并且具有相同的方法,特别地,它们实现了 Python 的数值运算符 +、-、*、//、%、divmod、**、== 和 !=。最后两个运算符由于浮点舍入误差可能有点问题。我们现在使用 NumPy 1.7.0 版快速演示各种操作。
基础知识#
首先,我们需要一个多项式类和一个多项式实例来进行操作。这些类可以直接从 `polynomial` 包或相关类型的模块中导入。在这里,我们从包中导入并使用传统的 `Polynomial` 类,因为其较为熟悉。
>>> from numpy.polynomial import Polynomial as P
>>> p = P([1,2,3])
>>> p
Polynomial([1., 2., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
请注意,打印输出的长版本有三个部分。第一个是系数,第二个是域,第三个是窗口。
>>> p.coef
array([1., 2., 3.])
>>> p.domain
array([-1., 1.])
>>> p.window
array([-1., 1.])
打印多项式会以更熟悉的格式显示多项式表达式。
>>> print(p)
1.0 + 2.0·x + 3.0·x²
请注意,多项式的字符串表示形式默认使用 Unicode 字符(Windows 除外)来表示幂和下标。也提供基于 ASCII 的表示形式(Windows 上的默认)。多项式字符串格式可以通过包级别的 set_default_printstyle 函数进行切换。
>>> np.polynomial.set_default_printstyle('ascii')
>>> print(p)
1.0 + 2.0 x + 3.0 x**2
或者通过字符串格式化来控制单个多项式实例。
>>> print(f"{p:unicode}")
1.0 + 2.0·x + 3.0·x²
我们将在拟合时处理域和窗口,目前我们先忽略它们,并介绍基本的代数和算术运算。
加法和减法
>>> p + p
Polynomial([2., 4., 6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p - p
Polynomial([0.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
乘法
>>> p * p
Polynomial([ 1., 4., 10., 12., 9.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
幂
>>> p**2
Polynomial([ 1., 4., 10., 12., 9.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
除法
整除运算符‘//’是多项式类的除法运算符,在这方面多项式被视为整数。对于 Python < 3.x 版本,‘/’运算符映射到‘//’,正如 Python 本身一样;对于更高版本,‘/’只适用于标量除法。在某个时候它将被弃用。
>>> p // P([-1, 1])
Polynomial([5., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
余数
>>> p % P([-1, 1])
Polynomial([6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
取商和余数
>>> quo, rem = divmod(p, P([-1, 1]))
>>> quo
Polynomial([5., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> rem
Polynomial([6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
求值
>>> x = np.arange(5)
>>> p(x)
array([ 1., 6., 17., 34., 57.])
>>> x = np.arange(6).reshape(3,2)
>>> p(x)
array([[ 1., 6.],
[17., 34.],
[57., 86.]])
替换
用一个多项式替换 x 并展开结果。在这里,我们将 p 自身代入,展开后得到一个 4 阶新多项式。如果将多项式视为函数,这相当于函数复合。
>>> p(p)
Polynomial([ 6., 16., 36., 36., 27.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
根
>>> p.roots()
array([-0.33333333-0.47140452j, -0.33333333+0.47140452j])
并非总是方便显式使用 Polynomial 实例,因此元组、列表、数组和标量在算术运算中会自动进行类型转换。
>>> p + [1, 2, 3]
Polynomial([2., 4., 6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> [1, 2, 3] * p
Polynomial([ 1., 4., 10., 12., 9.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p / 2
Polynomial([0.5, 1. , 1.5], domain=[-1., 1.], window=[-1., 1.], symbol='x')
在域、窗口或类上不同的多项式不能进行混合运算。
>>> from numpy.polynomial import Chebyshev as T
>>> p + P([1], domain=[0,1])
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<string>", line 213, in __add__
TypeError: Domains differ
>>> p + P([1], window=[0,1])
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<string>", line 215, in __add__
TypeError: Windows differ
>>> p + T([1])
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<string>", line 211, in __add__
TypeError: Polynomial types differ
但不同类型可用于替换。事实上,多项式类之间进行类型、域和窗口转换就是通过这种方式完成的。
>>> p(T([0, 1]))
Chebyshev([2.5, 2. , 1.5], domain=[-1., 1.], window=[-1., 1.], symbol='x')
这给出了切比雪夫形式的多项式 p。这是因为 \(T_1(x) = x\),并且用 \(x\) 替换 \(x\) 不会改变原始多项式。然而,所有的乘法和除法都将使用切比雪夫级数完成,因此结果的类型也会随之确定。
所有多项式实例都旨在保持不可变性,因此增强赋值操作(如 +=、-= 等)以及任何其他会破坏多项式实例不可变性的功能都被有意地未实现。
微积分#
多项式实例可以进行积分和微分。
>>> from numpy.polynomial import Polynomial as P
>>> p = P([2, 6])
>>> p.integ()
Polynomial([0., 2., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p.integ(2)
Polynomial([0., 0., 1., 1.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
第一个例子对 p 积分一次,第二个例子积分两次。默认情况下,积分的下限和积分常数均为 0,但两者都可以指定。
>>> p.integ(lbnd=-1)
Polynomial([-1., 2., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p.integ(lbnd=-1, k=1)
Polynomial([0., 2., 3.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
第一个例子中,积分下限设为 -1,积分常数为 0。第二个例子中,积分常数也设为 1。微分则更简单,因为唯一的选项是多项式被微分的次数。
>>> p = P([1, 2, 3])
>>> p.deriv(1)
Polynomial([2., 6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p.deriv(2)
Polynomial([6.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
其他多项式构造函数#
通过指定系数来构造多项式只是获取多项式实例的一种方式,它们也可以通过指定其根、从其他多项式类型转换以及通过最小二乘拟合来创建。拟合将在其专属章节中讨论,其他方法将在下面演示。
>>> from numpy.polynomial import Polynomial as P
>>> from numpy.polynomial import Chebyshev as T
>>> p = P.fromroots([1, 2, 3])
>>> p
Polynomial([-6., 11., -6., 1.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> p.convert(kind=T)
Chebyshev([-9. , 11.75, -3. , 0.25], domain=[-1., 1.], window=[-1., 1.], symbol='x')
`convert` 方法也可以转换域和窗口。
>>> p.convert(kind=T, domain=[0, 1])
Chebyshev([-2.4375 , 2.96875, -0.5625 , 0.03125], domain=[0., 1.], window=[-1., 1.], symbol='x')
>>> p.convert(kind=P, domain=[0, 1])
Polynomial([-1.875, 2.875, -1.125, 0.125], domain=[0., 1.], window=[-1., 1.], symbol='x')
在 NumPy 1.7.0 及更高版本中,还提供了 basis 和 cast 类方法。`cast` 方法的作用类似于 `convert` 方法,而 `basis` 方法返回给定次数的基多项式。
>>> P.basis(3)
Polynomial([0., 0., 0., 1.], domain=[-1., 1.], window=[-1., 1.], symbol='x')
>>> T.cast(p)
Chebyshev([-9. , 11.75, -3. , 0.25], domain=[-1., 1.], window=[-1., 1.], symbol='x')
类型之间的转换可能很有用,但*不*建议日常使用。将 50 阶切比雪夫级数转换为相同阶数的普通多项式级数时,数值精度损失可能使数值求值结果基本随机。
拟合#
拟合是 domain 和 window 属性成为便利类一部分的原因。为了说明问题,下面绘制了最高 5 阶切比雪夫多项式的值。
>>> import matplotlib.pyplot as plt
>>> from numpy.polynomial import Chebyshev as T
>>> x = np.linspace(-1, 1, 100)
>>> for i in range(6):
... ax = plt.plot(x, T.basis(i)(x), lw=2, label=f"$T_{i}$")
...
>>> plt.legend(loc="upper left")
>>> plt.show()
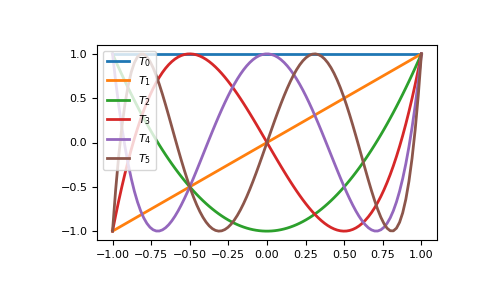
在 -1 <= x <= 1 的范围内,它们是良好的等波纹函数,值介于 +/- 1 之间。在 -2 <= x <= 2 的范围内,相同的图看起来非常不同。
>>> import matplotlib.pyplot as plt
>>> from numpy.polynomial import Chebyshev as T
>>> x = np.linspace(-2, 2, 100)
>>> for i in range(6):
... ax = plt.plot(x, T.basis(i)(x), lw=2, label=f"$T_{i}$")
...
>>> plt.legend(loc="lower right")
>>> plt.show()
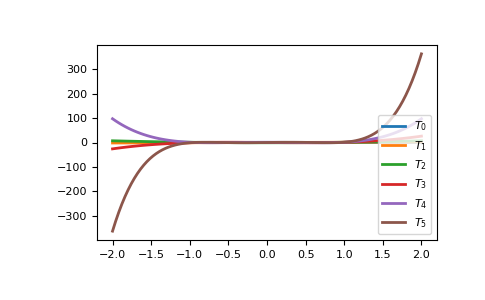
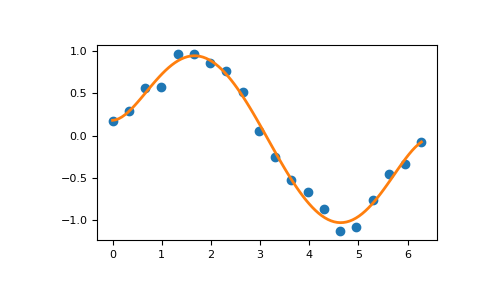
可以看出,“良好”的部分已经缩小到微不足道。在使用切比雪夫多项式进行拟合时,我们希望使用 x 介于 -1 和 1 之间的区域,这就是 window 所指定的。然而,要拟合的数据不太可能所有数据点都在该区间内,因此我们使用 domain 来指定数据点所在的区间。拟合完成后,域首先通过线性变换映射到窗口,然后使用映射后的数据点进行通常的最小二乘拟合。拟合的窗口和域是返回级数的一部分,在计算值、导数等时会自动使用。如果在调用中未指定它们,拟合例程将使用默认窗口和包含所有数据点最小的域。下面通过拟合一条带噪声的正弦曲线来演示这一点。
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from numpy.polynomial import Chebyshev as T
>>> np.random.seed(11)
>>> x = np.linspace(0, 2*np.pi, 20)
>>> y = np.sin(x) + np.random.normal(scale=.1, size=x.shape)
>>> p = T.fit(x, y, 5)
>>> plt.plot(x, y, 'o')
>>> xx, yy = p.linspace()
>>> plt.plot(xx, yy, lw=2)
>>> p.domain
array([0. , 6.28318531])
>>> p.window
array([-1., 1.])
>>> plt.show()