使用 NumPy 中的真实数据确定摩尔定律#

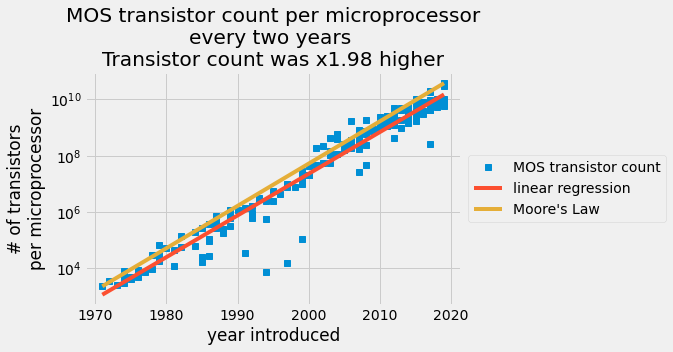
Scatter plot of MOS transistor count per microprocessor every two years as a demonstration of Moore's Law.

每个给定芯片报告的晶体管数量在 y 轴上以对数刻度绘制，在 x 轴上以线性刻度绘制引入日期。蓝色数据点来自晶体管计数表。红线是普通最小二乘预测，橙线是摩尔定律。

您将做什么#

1965 年，工程师戈登·摩尔预测芯片上的晶体管数量将在未来十年内每两年翻一番 [1]。您将比较摩尔的预测与他预测后 53 年内的实际晶体管数量。您将确定最佳拟合常数，以描述半导体上晶体管的指数增长与摩尔定律的比较。

您将学到的技能#

从 *.csv 文件加载数据
执行线性回归并使用普通最小二乘法预测指数增长
您将比较模型之间的指数增长常数
将您的分析保存到文件中
- 作为 NumPy 压缩文件 *.npz
- 作为 *.csv 文件
评估半导体制造商在过去五十年中取得的惊人进展

您需要什么#

1. 这些包

NumPy
Matplotlib

使用以下命令导入

import matplotlib.pyplot as plt
import numpy as np

2. 由于这是一个指数增长定律，您需要一些关于使用自然对数和指数进行数学运算的背景知识。

您将使用这些 NumPy 和 Matplotlib 函数

np.loadtxt：此函数将文本加载到 NumPy 数组中
np.log：此函数获取 NumPy 数组中所有元素的自然对数
np.exp：此函数获取 NumPy 数组中所有元素的指数
lambda：这是一个用于创建函数模型的最小函数定义
plt.semilogy：此函数将 x-y 数据绘制到图形上，其中 x 轴是线性刻度，y 轴是 $\log_{10}$ 对数刻度 plt.plot：此函数将在线性轴上绘制 x-y 数据
数组切片：查看加载到工作区中的数据部分，切片数组，例如 x[:10] 表示数组 x 中的前 10 个值
布尔数组索引：要查看符合给定条件的数据部分，请使用布尔运算对数组进行索引
np.block：将数组组合成二维数组
np.newaxis：将一维向量更改为行向量或列向量
np.savez 和 np.savetxt：这两个函数将分别以压缩数组格式和文本格式保存您的数组

将摩尔定律构建为指数函数#

您的经验模型假设每半导体的晶体管数量遵循指数增长，

$\log(\text{transistor_count})= f(\text{year}) = A\cdot \text{year}+B,$

其中 $A$ 和 $B$ 是拟合常数。您使用半导体制造商的数据来找到拟合常数。

您通过指定晶体管的增加速率（2）并给出给定年份的初始晶体管数量来确定摩尔定律的这些常数。

您将摩尔定律以指数形式表述如下：

$\text{transistor_count}= e^{A_M\cdot \text{year} +B_M}.$

其中 $A_M$ 和 $B_M$ 是使晶体管数量每两年翻一番并于 1971 年从 2250 个晶体管开始的常数，

$\dfrac{\text{transistor_count}(\text{year} +2)}{\text{transistor_count}(\text{year})} = 2 = \dfrac{e^{B_M}e^{A_M \text{year} + 2A_M}}{e^{B_M}e^{A_M \text{year}}} = e^{2A_M} \rightarrow A_M = \frac{\log(2)}{2}$
$\log(2250) = \frac{\log(2)}{2}\cdot 1971 + B_M \rightarrow B_M = \log(2250)-\frac{\log(2)}{2}\cdot 1971$

因此，摩尔定律表述为指数函数为

$\log(\text{transistor_count})= A_M\cdot \text{year}+B_M,$

其中

$A_M=0.3466$

$B_M=-675.4$

由于该函数代表摩尔定律，请使用 lambda 将其定义为 Python 函数

A_M = np.log(2) / 2
B_M = np.log(2250) - A_M * 1971
Moores_law = lambda year: np.exp(B_M) * np.exp(A_M * year)

1971 年，Intel 4004 芯片上有 2250 个晶体管。使用 Moores_law 检查戈登·摩尔预计 1973 年的半导体数量。

ML_1971 = Moores_law(1971)
ML_1973 = Moores_law(1973)
print("In 1973, G. Moore expects {:.0f} transistors on Intels chips".format(ML_1973))
print("This is x{:.2f} more transistors than 1971".format(ML_1973 / ML_1971))

In 1973, G. Moore expects 4500 transistors on Intels chips
This is x2.00 more transistors than 1971

将历史制造数据加载到您的工作区#

现在，根据每个芯片半导体的历史数据进行预测。每年晶体管计数[3]位于 transistor_data.csv 文件中。在将 *.csv 文件加载到 NumPy 数组之前，最好先检查文件的结构。然后，找到感兴趣的列并将它们保存到变量中。将文件的两列保存到数组 data 中。

在此，打印出 transistor_data.csv 的前 10 行。列为

处理器	MOS 晶体管计数	引入日期	设计者	MOS工艺	面积
Intel 4004 (4位 16引脚)	2250	1971	Intel	“10,000 纳米”	12 平方毫米
…	…	…	…	…	…

! head transistor_data.csv

Processor,MOS transistor count,Date of Introduction,Designer,MOSprocess,Area
Intel 4004 (4-bit  16-pin),2250,1971,Intel,"10,000 nm",12 mm²
Intel 8008 (8-bit  18-pin),3500,1972,Intel,"10,000 nm",14 mm²
NEC μCOM-4 (4-bit  42-pin),2500,1973,NEC,"7,500 nm",?
Intel 4040 (4-bit  16-pin),3000,1974,Intel,"10,000 nm",12 mm²
Motorola 6800 (8-bit  40-pin),4100,1974,Motorola,"6,000 nm",16 mm²
Intel 8080 (8-bit  40-pin),6000,1974,Intel,"6,000 nm",20 mm²
TMS 1000 (4-bit  28-pin),8000,1974,Texas Instruments,"8,000 nm",11 mm²
MOS Technology 6502 (8-bit  40-pin),4528,1975,MOS Technology,"8,000 nm",21 mm²
Intersil IM6100 (12-bit  40-pin; clone of PDP-8),4000,1975,Intersil,,

您不需要指定处理器、设计者、MOS工艺或面积的列。因此剩下第二列和第三列，分别为MOS晶体管计数和引入日期。

接下来，您使用 np.loadtxt 将这两列加载到 NumPy 数组中。下面的额外选项将使数据符合所需的格式

delimiter = ','：指定分隔符为逗号 ','（这是默认行为）
usecols = [1,2]：从 csv 导入第二列和第三列
skiprows = 1：不使用第一行，因为它是一个标题行

data = np.loadtxt("transistor_data.csv", delimiter=",", usecols=[1, 2], skiprows=1)

您已将半导体的整个历史记录加载到名为 data 的 NumPy 数组中。第一列是 MOS 晶体管计数，第二列是四位数字年份的引入日期。

接下来，通过将两列分配给变量 year 和 transistor_count，使数据更易于阅读和管理。通过使用 [:10] 对 year 和 transistor_count 数组进行切片，打印出前 10 个值。打印出这些值以检查您是否已将数据保存到正确的变量中。

year = data[:, 1]  # grab the second column and assign
transistor_count = data[:, 0]  # grab the first column and assign

print("year:\t\t", year[:10])
print("trans. cnt:\t", transistor_count[:10])

year:		 [1971. 1972. 1973. 1974. 1974. 1974. 1974. 1975. 1975. 1975.]
trans. cnt:	 [2250. 3500. 2500. 3000. 4100. 6000. 8000. 4528. 4000. 5000.]

您正在创建一个根据年份预测晶体管数量的函数。您有一个自变量year 和一个因变量transistor_count。将因变量转换为对数尺度，

$y_i = \log($ transistor_count[i] $),$

得到一个线性方程，

$y_i = A\cdot \text{year} +B$.

yi = np.log(transistor_count)

计算晶体管的历史增长曲线#

您的模型假设 yi 是 year 的函数。现在，找到使 $y_i$ 和 $A\cdot \text{year} +B, $ 之间差异最小的最佳拟合模型，如下所示

$\min \sum|y_i - (A\cdot \text{year}_i + B)|^2.$

这种平方误差和可以用数组简洁地表示为

$\sum|\mathbf{y}-\mathbf{Z} [A,~B]^T|^2,$

其中 $\mathbf{y}$ 是晶体管数量对数的观测值（一维数组），而 $\mathbf{Z}=[\text{year}_i^1,~\text{year}_i^0]$ 是第一列和第二列中 $\text{year}_i$ 的多项式项。通过在 $\mathbf{Z}-$ 矩阵中创建这组回归量，您建立了一个普通最小二乘统计模型。

Z 是一个具有两个参数的线性模型，即度数为 1 的多项式。因此，我们可以用 numpy.polynomial.Polynomial 来表示模型，并使用拟合功能来确定模型参数

model = np.polynomial.Polynomial.fit(year, yi, deg=1)

默认情况下，Polynomial.fit 在由自变量（在本例中为 year）确定的域中执行拟合。未缩放和未平移模型的系数可以通过 convert 方法恢复

model = model.convert()
model

\[x \mapsto \text{-666.32640635} + \text{0.34163208}\,x\]

单个参数 $A$ 和 $B$ 是我们线性模型的系数

B, A = model

制造商是否每两年将晶体管数量翻一番？您有最终公式，

$\dfrac{\text{transistor_count}(\text{year} +2)}{\text{transistor_count}(\text{year})} = xFactor = \dfrac{e^{B}e^{A( \text{year} + 2)}}{e^{B}e^{A \text{year}}} = e^{2A}$

其中晶体管数量的增加为 $xFactor,$ 年数为 2，$A$ 是半对数函数上的最佳拟合斜率。

print(f"Rate of semiconductors added on a chip every 2 years: {np.exp(2 * A):.2f}")

Rate of semiconductors added on a chip every 2 years: 1.98

根据您的最小二乘回归模型，每块芯片的半导体数量每两年增长 $1.98$ 倍。您有一个模型可以预测每年半导体的数量。现在将您的模型与实际制造报告进行比较。绘制线性回归结果和所有晶体管计数。

在这里，使用 plt.semilogy 以对数刻度绘制晶体管数量，以线性刻度绘制年份。您已定义三个数组以获得最终模型

$y_i = \log(\text{transistor_count}),$

$y_i = A \cdot \text{year} + B,$

和

$\log(\text{transistor_count}) = A\cdot \text{year} + B,$

您的变量 transistor_count、year 和 yi 都具有相同的维度，(179,)。NumPy 数组需要相同的维度才能绘制图表。现在预测的晶体管数量是

$\text{transistor_count}_{\text{predicted}} = e^Be^{A\cdot \text{year}}$.

在下一个图中，使用 fivethirtyeight 样式表。该样式表复制了 https://fivethirtyeight.com 的元素。使用 plt.style.use 更改 matplotlib 样式。

transistor_count_predicted = np.exp(B) * np.exp(A * year)
transistor_Moores_law = Moores_law(year)
plt.style.use("fivethirtyeight")
plt.semilogy(year, transistor_count, "s", label="MOS transistor count")
plt.semilogy(year, transistor_count_predicted, label="linear regression")


plt.plot(year, transistor_Moores_law, label="Moore's Law")
plt.title(
    "MOS transistor count per microprocessor\n"
    + "every two years \n"
    + "Transistor count was x{:.2f} higher".format(np.exp(A * 2))
)
plt.xlabel("year introduced")
plt.legend(loc="center left", bbox_to_anchor=(1, 0.5))
plt.ylabel("# of transistors\nper microprocessor")

Text(0, 0.5, '# of transistors\nper microprocessor')

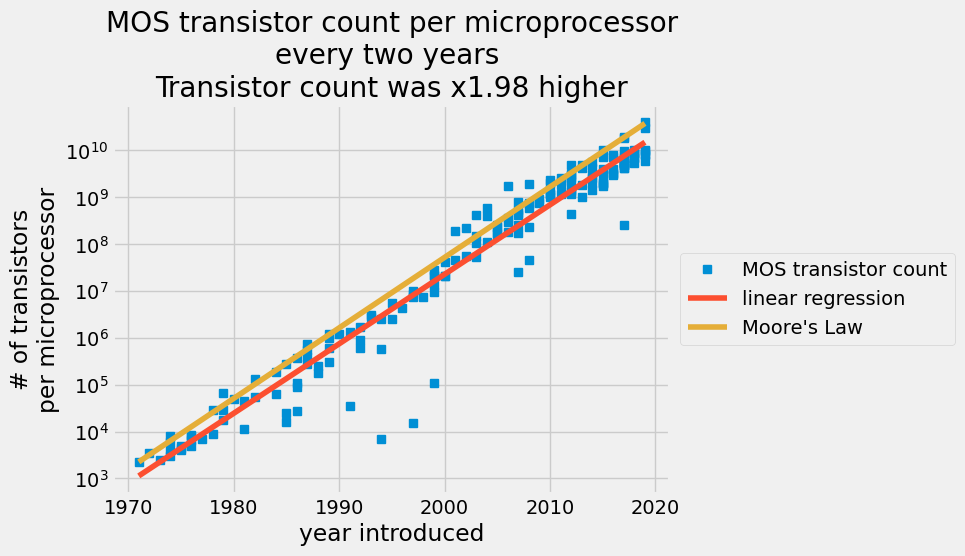
../_images/672fa8d81d580c45cc84a257437ca1e0dcae3eabe4ada6b09221b98dbcdc6132.png

每两年每微处理器 MOS 晶体管数量的散点图，红线表示普通最小二乘预测，橙线表示摩尔定律。

线性回归捕捉了每年每半导体晶体管数量的增长。2015年，半导体制造商声称他们无法再跟上摩尔定律。您的分析表明，自1971年以来，晶体管数量的平均增长每两年增加1.98倍，而戈登·摩尔预测每两年增加2倍。这是一个惊人的预测。

考虑 2017 年。将数据与您的线性回归模型和戈登·摩尔的预测进行比较。首先，获取 2017 年的晶体管计数。您可以使用布尔比较器来完成此操作，

year == 2017.

然后，用上面定义的 Moores_law 并将您最佳拟合的常数代入您的函数来预测 2017 年

$\text{transistor_count} = e^{B}e^{A\cdot \text{year}}$.

比较这些测量值的一个好方法是将您的预测和摩尔的预测与平均晶体管计数进行比较，并查看当年报告值的范围。使用 plt.plot 选项 alpha=0.2 来增加数据的透明度。点越不透明，表示在该测量值上报告的值越多。绿色 $+$ 是 2017 年报告的平均晶体管计数。绘制您对 $\pm\frac{1}{2}~years$ 的预测。

transistor_count2017 = transistor_count[year == 2017]
print(
    transistor_count2017.max(), transistor_count2017.min(), transistor_count2017.mean()
)
y = np.linspace(2016.5, 2017.5)
your_model2017 = np.exp(B) * np.exp(A * y)
Moore_Model2017 = Moores_law(y)

plt.plot(
    2017 * np.ones(np.sum(year == 2017)),
    transistor_count2017,
    "ro",
    label="2017",
    alpha=0.2,
)
plt.plot(2017, transistor_count2017.mean(), "g+", markersize=20, mew=6)

plt.plot(y, your_model2017, label="Your prediction")
plt.plot(y, Moore_Model2017, label="Moores law")
plt.ylabel("# of transistors\nper microprocessor")
plt.legend()

19200000000.0 250000000.0 7050000000.0

<matplotlib.legend.Legend at 0x7fa70c3043d0>

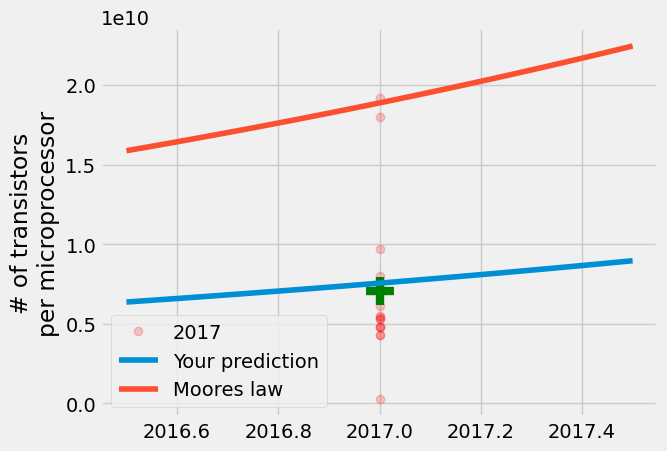
../_images/52ecc05d3a5663f3bd9c76d16b0ed82dd38d03ad17a00b965c0e4e83d5a98a24.png

结果是您的模型接近平均值，但戈登·摩尔的预测更接近 2017 年生产的每微处理器最大晶体管数量。尽管半导体制造商认为增长会放缓，在 1975 年和现在接近 2025 年时，制造商仍然每两年生产的半导体晶体管数量几乎翻倍。

线性回归模型在预测平均值方面远优于预测极端值，因为它满足了最小化 $\sum |y_i - A\cdot \text{year}[i]+B|^2$ 的条件。

总结#

总而言之，您已经比较了半导体制造商的历史数据与摩尔定律，并创建了一个线性回归模型来找出每两年添加到每个微处理器的平均晶体管数量。戈登·摩尔预测从 1965 年到 1975 年，晶体管数量将每两年翻一番，但从 1971 年到 2019 年，平均增长一直保持在每两年 $\times 1.98 \pm 0.01$。2015 年，摩尔修正了他的预测，称摩尔定律应持续到 2025 年。 [2]。您可以将这些结果分享为压缩的 NumPy 数组文件 mooreslaw_regression.npz，或另一个 csv 文件 mooreslaw_regression.csv。半导体制造的惊人进展催生了新产业和计算能力的提升。这项分析应该能让您对过去半个世纪以来这种令人难以置信的增长有一个小小的洞察。

使用 NumPy 中的真实数据确定摩尔定律

目录

使用 NumPy 中的真实数据确定摩尔定律#

您将做什么#

您将学到的技能#

您需要什么#

将摩尔定律构建为指数函数#

将历史制造数据加载到您的工作区#

计算晶体管的历史增长曲线#

总结#

参考文献#

使用 NumPy 中的真实数据确定摩尔定律

目录

使用 NumPy 中的真实数据确定摩尔定律#

您将做什么#

您将学到的技能#

您需要什么#

将摩尔定律构建为指数函数#

将历史制造数据加载到您的工作区#

计算晶体管的历史增长曲线#

将您的结果作为压缩数组和 CSV 文件共享#

将数组压缩到文件中#

创建您自己的逗号分隔值文件#

总结#

参考文献#