n维数组上的线性代数

先决条件¶

在阅读本教程之前，你应该对Python有所了解。如果你想回顾一下，可以看看Python教程。

如果你想运行本教程中的示例，你还应该在计算机上安装matplotlib和SciPy。

学习者画像¶

本教程适合那些对NumPy中的线性代数和数组有基本了解，并希望理解n维（$n>=2$）数组是如何表示和操作的人。特别是，如果你不知道如何在n维数组上应用常用函数（不使用for循环），或者你想理解n维数组的轴（axis）和形状（shape）属性，本教程可能会有所帮助。

学习目标¶

在本教程结束后，你应该能够

• 理解NumPy中一维、二维和n维数组的区别；

• 理解如何在不使用for循环的情况下，将一些线性代数运算应用于n维数组；

• 理解n维数组的轴和形状属性。

内容¶

在本教程中，我们将使用线性代数中的矩阵分解——奇异值分解（Singular Value Decomposition），来生成图像的压缩近似。我们将使用scipy.datasets模块中的face图像。

from scipy.datasets import face

img = face()

Downloading file 'face.dat' from 'https://raw.githubusercontent.com/scipy/dataset-face/main/face.dat' to '/home/runner/.cache/scipy-data'.

现在，img是一个NumPy数组，我们可以通过使用type函数看到这一点。

type(img)

我们可以使用matplotlib.pyplot.imshow函数和特殊的iPython命令%matplotlib inline来显示图像，并将图内联显示。

import matplotlib.pyplot as plt

%matplotlib inline

plt.imshow(img)
plt.show()

形状、轴和数组属性¶

请注意，在线性代数中，向量的维度是指数组中的元素数量。而在NumPy中，它定义了轴的数量。例如，一维数组是向量，如[1, 2, 3]；二维数组是矩阵，以此类推。

首先，我们检查数组中数据的形状。由于这张图像是二维的（图像中的像素形成一个矩形），我们可能会期望一个二维数组来表示它（一个矩阵）。然而，使用这个NumPy数组的shape属性会给我们一个不同的结果。

img.shape

输出是一个包含三个元素的元组，这意味着这是一个三维数组。由于这是一张彩色图像，并且我们使用imread函数读取了它，数据被组织成一个768×1024的像素网格，其中每个像素包含3个代表颜色通道（红、绿、蓝——RGB）的值。你可以通过查看形状来看到这一点，最左边的数字对应最外层的轴（图像高度），中间的数字对应下一个轴（图像宽度），最右边的数字对应最内层的轴（颜色通道）。

此外，使用这个数组的ndim属性，我们可以看到

img.ndim

NumPy将每个维度称为一个轴。由于imread的工作方式，第三个轴的第一个索引是我们图像的红色像素数据。我们可以使用以下语法访问它：

img[:, :, 0]

从上面的输出中，我们可以看到img[:, :, 0]中的每个值都是0到255之间的整数，代表我们图像中每个相应像素的红色级别（请记住，如果你使用自己的图像而不是scipy.datasets.face，结果可能会有所不同）。

正如预期的那样，这是一个768x1024的矩阵。

img[:, :, 0].shape

由于我们将在此数据上执行线性代数运算，因此可能更有趣的是，让每个矩阵的条目是介于0和1之间的实数，以表示RGB值。我们可以通过设置来实现：

img_array = img / 255

此操作，即用标量除以数组，之所以有效，是因为NumPy的广播规则。

你可以通过一些测试来验证上述操作是否有效；例如，查询该数组的最大值和最小值。

img_array.min(), img_array.max()

或者检查数组中数据的类型。

img_array.dtype

请注意，我们可以使用切片语法将每个颜色通道分配给一个单独的矩阵。

red_array = img_array[:, :, 0]
green_array = img_array[:, :, 1]
blue_array = img_array[:, :, 2]

沿轴进行运算¶

可以使用线性代数方法来近似现有数据集。在这里，我们将使用SVD（奇异值分解）来尝试重建一个使用比原始图像更少的奇异值信息的图像，同时仍然保留其部分特征。

为了从给定矩阵中提取信息，我们可以使用SVD得到3个数组，它们相乘可以得到原始矩阵。根据线性代数理论，给定一个矩阵$A$，可以计算以下乘积：

其中$U$和$V^T$是方阵，而$\Sigma$的尺寸与$A$相同。$\Sigma$是一个对角矩阵，包含$A$的奇异值，按从大到小的顺序排列。这些值始终是非负的，并且可以作为矩阵$A$所表示的某些特征的“重要性”的指标。

让我们先用一个矩阵来看看它是如何工作的。请注意，根据色度学，通过应用以下公式可以得到一个相当合理颜色的灰度版本：

其中$Y$是表示灰度图像的数组，而$R$、$G$和$B$是我们最初的红、绿、蓝通道数组。注意，我们可以使用@运算符（NumPy数组的矩阵乘法运算符，请参阅numpy.matmul）来实现这一点。

img_gray = img_array @ [0.2126, 0.7152, 0.0722]

现在，img_gray的形状是

img_gray.shape

为了在图像中看到是否有意义，我们应该使用matplotlib中的一个颜色映射，该颜色映射与我们希望在图像中看到的颜色相对应（否则，matplotlib将默认为一个与真实数据不对应的颜色映射）。

在我们的例子中，我们正在近似图像的灰度部分，所以我们将使用gray颜色映射。

plt.imshow(img_gray, cmap="gray")
plt.show()

现在，对这个矩阵应用linalg.svd函数，我们得到以下分解：

import numpy as np
U, s, Vt = np.linalg.svd(img_gray)

让我们检查一下这是否是我们期望的结果。

U.shape, s.shape, Vt.shape

请注意，s有一个特殊的形状：它只有一个维度。这意味着一些期望二维数组的线性代数函数可能无法正常工作。例如，根据理论，你可能期望s和Vt能够相乘。然而，这是不正确的，因为s没有第二个轴。

s @ Vt

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[18], line 1
----> 1 s @ Vt

ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 1024 is different from 768)

会导致ValueError。发生这种情况是因为在这种情况下，使用一维数组s比构建一个具有相同数据的对角矩阵在实践中要经济得多。要重构原始矩阵，我们可以使用s中的元素构建对角矩阵$\Sigma$，并具有适当的乘法尺寸：在我们的例子中，因为U是768x768，而Vt是1024x1024，所以$\Sigma$应该是768x1024。为了将奇异值添加到Sigma的对角线上，我们将使用NumPy中的fill_diagonal函数。

Sigma = np.zeros((U.shape[1], Vt.shape[0]))
np.fill_diagonal(Sigma, s)

现在，我们要检查重构的U @ Sigma @ Vt是否接近原始的img_gray矩阵。

近似¶

linalg模块包含一个norm函数，它计算NumPy数组表示的向量或矩阵的范数。例如，根据上面的SVD解释，我们期望img_gray与重构的SVD乘积之间的差值的范数很小。正如预期的那样，你应该看到类似这样的结果：

np.linalg.norm(img_gray - U @ Sigma @ Vt)

(此操作的实际结果可能因你的架构和线性代数设置而异。无论如何，你应该看到一个小的数字)。

我们也可以使用numpy.allclose函数来确保重构的乘积实际上接近我们的原始矩阵（两个数组之间的差异很小）。

np.allclose(img_gray, U @ Sigma @ Vt)

为了查看近似是否合理，我们可以检查s中的值。

plt.plot(s)
plt.show()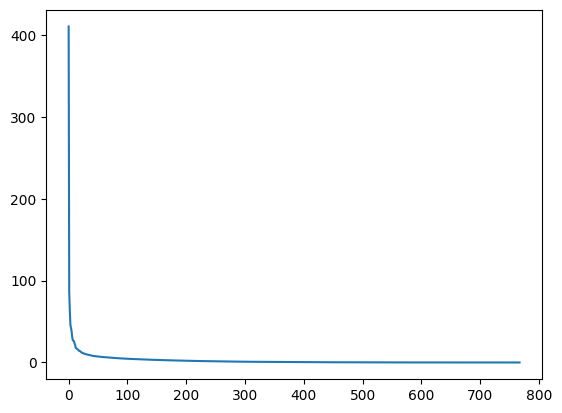

在图中，我们可以看到，尽管s中有768个奇异值，但其中大部分（大约在第150个条目之后）非常小。所以，只使用与前（例如，50个）*奇异值*相关的信息来构建一个更节省空间的图像近似可能是有意义的。

思路是考虑Sigma中（与s相同）除前k个奇异值之外的所有值都为零，保持U和Vt不变，然后计算这些矩阵的乘积作为近似。

例如，如果我们选择

k = 10

我们可以通过以下方式构建近似：

approx = U @ Sigma[:, :k] @ Vt[:k, :]

请注意，我们只需要使用Vt的前k行，因为所有其他行都将乘以对应于我们从此近似中消除的奇异值的零。因此，我们选择Vt的前k行。

plt.imshow(approx, cmap="gray")
plt.show()

现在，你可以尝试用其他k值重复这个实验，每次实验都应该给你一个略好（或更差）的图像，这取决于你选择的值。

应用于所有颜色¶

现在我们要对所有三种颜色进行相同的操作。我们最初的想法可能是单独对每个颜色矩阵重复上述操作。然而，NumPy的*广播*会为我们处理这个问题。

如果我们的数组维度大于2，那么SVD可以一次应用于所有轴。然而，NumPy中的线性代数函数期望看到形状为(n, M, N)的数组，其中第一个轴n表示堆栈中MxN矩阵的数量。

在我们的例子中，

img_array.shape

所以我们需要置换这个数组的轴，以获得形状如(3, 768, 1024)的形式。幸运的是，numpy.transpose函数可以为我们做到这一点。

# The values in the tuple indicate the original dim, and the order the new axis
# so axis 2 -> 0, 0 -> 1, and 1 -> 2
img_array_transposed = np.transpose(img_array, (2, 0, 1))
img_array_transposed.shape

现在我们准备应用SVD。

U, s, Vt = np.linalg.svd(img_array_transposed)

最后，为了得到完整的近似图像，我们需要将这些矩阵重新组合成近似。现在，请注意：

U.shape, s.shape, Vt.shape

要构建最终的近似矩阵，我们必须理解跨不同轴的乘法是如何工作的。

n维数组的乘积¶

如果你以前只在NumPy中使用过一维或二维数组，你可能可能会将numpy.dot和numpy.matmul（或@运算符）混用。然而，对于n维数组，它们的行为非常不同。更多细节，请查阅关于numpy.matmul的文档。

现在，为了构建我们的近似，我们首先需要确保我们的奇异值已准备好进行乘法，所以我们构建Sigma矩阵，类似于我们之前所做的。Sigma数组必须具有(3, 768, 1024)的尺寸。为了将奇异值添加到Sigma的对角线上，我们将再次使用fill_diagonal函数，使用s中的每个3行作为Sigma中每个3个矩阵的对角线。

Sigma = np.zeros((3, 768, 1024))
for j in range(3):
    np.fill_diagonal(Sigma[j, :, :], s[j, :])

现在，如果我们想重建完整的SVD（无近似），我们可以这样做：

reconstructed = U @ Sigma @ Vt

请注意：

reconstructed.shape

重构的图像应该与原始图像无法区分，除了由于重构过程中的浮点误差而产生的差异。回想一下，我们的原始图像由范围在[0., 1.]之间的浮点值组成。重构过程中浮点误差的累积可能导致值略微超出此原始范围。

reconstructed.min(), reconstructed.max()

由于imshow期望范围内的值，我们可以使用clip来去除浮点误差。

reconstructed = np.clip(reconstructed, 0, 1)
plt.imshow(np.transpose(reconstructed, (1, 2, 0)))
plt.show()

现在，为了进行近似，我们必须为每个颜色通道只选择前k个奇异值。这可以通过以下语法完成：

approx_img = U @ Sigma[..., :k] @ Vt[..., :k, :]

你可以看到，我们只为Sigma的最后一个轴选择了前k个分量（这意味着我们只使用了堆栈中每个3个矩阵的前k列），并且我们为Vt的倒数第二个轴选择了前k个分量（这意味着我们从堆栈Vt的每个矩阵中选择了前k行，以及所有列）。如果你不熟悉省略号语法，它是一个占位符，代表其他轴。更多详情，请参阅*索引*文档：Indexing。

现在，

approx_img.shape

这不适合显示图像。最后，将轴重新排序回我们原来的形状(768, 1024, 3)，我们可以看到我们的近似。

plt.imshow(np.transpose(np.clip(approx_img, 0, 1), (1, 2, 0)))
plt.show()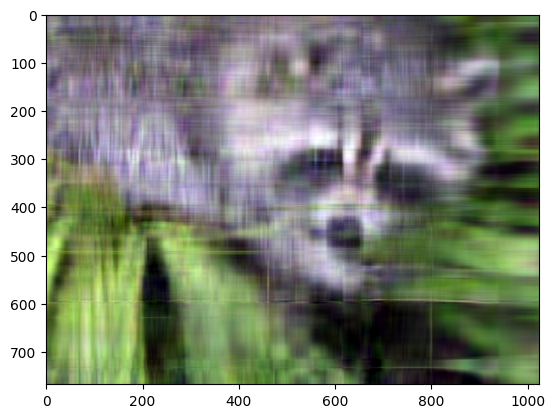

尽管图像不够清晰，但使用少量k奇异值（与原始768个值相比），我们可以恢复这张图像的许多显著特征。

结语¶

当然，这并不是*近似*图像的最佳方法。然而，线性代数中确实有一个结果表明，我们上面构建的近似在差值范数方面是最好的。更多信息，请参阅G. H. Golub and C. F. Van Loan, Matrix Computations, Baltimore, MD, Johns Hopkins University Press, 1985。

进一步阅读¶

• Python教程

• NumPy参考

• SciPy教程

• SciPy讲义

• Matlab, R, IDL, NumPy/SciPy词典