分析封锁对印度德里空气质量的影响

A grid showing the India Gate in smog above and clear air below

您将做什么¶

计算空气质量指数（AQI）并对其进行配对学生 t 检验。

您将学到什么¶

您将了解移动平均的概念
您将学习如何计算空气质量指数 (AQI)
您将学习如何执行配对学生 t 检验并找出 t 值和 p 值
您将学习如何解释这些值

您将需要什么¶

您的环境中已安装 SciPy
对诸如总体、样本、均值、标准差等统计术语有基本了解。

空气污染问题¶

空气污染是我们面临的最突出的污染类型之一，它对我们的日常生活有直接影响。COVID-19 大流行导致世界各地不同地区实施封锁；这提供了一个难得的机会来研究人类活动（或缺乏活动）对空气污染的影响。在本教程中，我们将研究德里（受空气污染影响最严重的城市之一）在 2020 年 3 月至 6 月封锁之前和期间的空气质量。为此，我们将首先根据收集到的污染物测量值计算每小时的空气质量指数。接下来，我们将对这些指数进行抽样，并对它们进行配对学生 t 检验。这将从统计上证明空气质量因封锁而有所改善，支持我们的直觉。

让我们开始将必要的库导入到我们的环境中。

import numpy as np
from numpy.random import default_rng
from scipy import stats

构建数据集¶

我们将使用精简版的印度空气质量数据数据集。该数据集包含印度多个城市各站点每小时和每天的空气质量数据和 AQI（空气质量指数）。本教程提供的精简版包含 2019 年 5 月 31 日至 2020 年 6 月 30 日德里每小时的污染物测量值。它包含计算空气质量指数所需的标准污染物以及其他一些重要污染物的测量值：颗粒物（PM 2.5 和 PM 10）、二氧化氮（NO2）、氨气（NH3）、二氧化硫（SO2）、一氧化碳（CO）、臭氧（O3）、氮氧化物（NOx）、一氧化氮（NO）、苯、甲苯和二甲苯。

让我们打印出前几行，以便对我们的数据集有一个初步了解。

! head air-quality-data.csv

Datetime,PM2.5,PM10,NO2,NH3,SO2,CO,O3,NOx,NO,Benzene,Toluene,Xylene
2019-05-31 00:00:00,103.26,305.46,94.71,31.43,30.16,3.0,18.06,178.31,152.73,13.65,83.47,2.54
2019-05-31 01:00:00,104.47,309.14,74.66,34.08,27.02,1.69,18.65,106.5,79.98,11.35,76.79,2.91
2019-05-31 02:00:00,90.0,314.02,48.11,32.6,18.12,0.83,28.27,48.45,25.27,5.66,32.91,1.59
2019-05-31 03:00:00,78.01,356.14,45.45,30.21,16.78,0.79,27.47,44.22,21.5,3.6,21.41,0.78
2019-05-31 04:00:00,80.19,372.9,45.23,28.68,16.41,0.76,26.92,44.06,22.15,4.5,23.39,0.62
2019-05-31 05:00:00,83.59,389.97,39.49,27.71,17.42,0.76,28.71,39.33,21.04,3.25,23.59,0.56
2019-05-31 06:00:00,79.04,371.64,39.61,26.87,16.91,0.84,29.26,43.11,24.37,3.12,15.27,0.46
2019-05-31 07:00:00,77.32,361.88,42.63,27.26,17.86,0.96,27.07,48.22,28.81,3.32,14.42,0.41
2019-05-31 08:00:00,84.3,377.77,42.49,28.41,20.19,0.98,33.05,48.22,27.76,3.4,14.53,0.4

在本教程中，我们只关心计算 AQI 所需的标准污染物，即 PM 2.5、PM 10、NO2、NH3、SO2、CO 和 O3。因此，我们将只使用np.loadtxt导入这些特定列。然后，我们将切片并创建两个集合：pollutants_A 包含 PM 2.5、PM 10、NO2、NH3 和 SO2，pollutants_B 包含 CO 和 O3。正如稍后将看到的，这两个集合将以略微不同的方式处理。

pollutant_data = np.loadtxt("air-quality-data.csv", dtype=float, delimiter=",",
                            skiprows=1, usecols=range(1, 8))
pollutants_A = pollutant_data[:, 0:5]
pollutants_B = pollutant_data[:, 5:]

print(pollutants_A.shape)
print(pollutants_B.shape)

(9528, 5)
(9528, 2)

我们的数据集可能包含 NaN 表示的缺失值，所以让我们用np.isfinite快速检查一下。

np.all(np.isfinite(pollutant_data))

np.True_

至此，我们已成功导入数据并确认其完整性。让我们继续进行 AQI 计算！

计算空气质量指数¶

我们将使用印度中央污染控制委员会采用的方法来计算 AQI。总结步骤如下：

收集标准污染物 24 小时平均浓度值；CO 和 O3 为 8 小时。
使用以下公式计算这些污染物的子指数
$Ip = \dfrac{\text{IHi – ILo}}{\text{BPHi – BPLo}}\cdot{\text{Cp – BPLo}} + \text{ILo}$
(1)
其中，
Ip = 污染物 p 的子指数
Cp = 污染物 p 的平均浓度
BPHi = 浓度断点，即大于或等于 Cp
BPLo = 浓度断点，即小于或等于 Cp
IHi = 与 BPHi 对应的 AQI 值
ILo = 与 BPLo 对应的 AQI 值
任何给定时间的最大子指数就是空气质量指数。

空气质量指数是借助下图中所示的断点范围计算的。

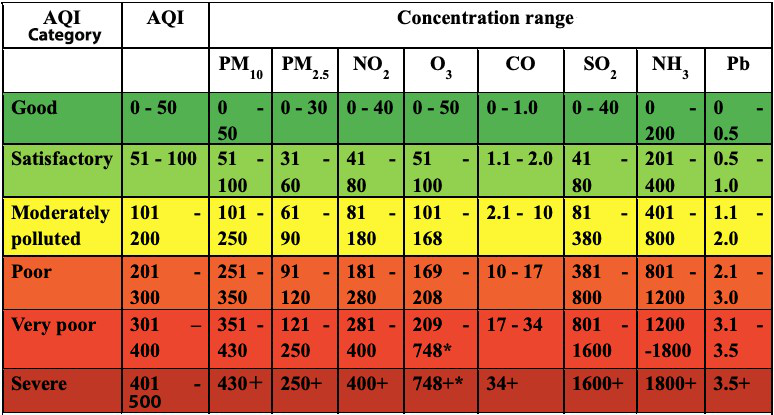
让我们创建两个数组来存储 AQI 范围和断点，以便稍后用于计算。

AQI = np.array([0, 51, 101, 201, 301, 401, 501])

breakpoints = {
    'PM2.5': np.array([0, 31, 61, 91, 121, 251]),
    'PM10': np.array([0, 51, 101, 251, 351, 431]),
    'NO2': np.array([0, 41, 81, 181, 281, 401]),
    'NH3': np.array([0, 201, 401, 801, 1201, 1801]),
    'SO2': np.array([0, 41, 81, 381, 801, 1601]),
    'CO': np.array([0, 1.1, 2.1, 10.1, 17.1, 35]),
    'O3': np.array([0, 51, 101, 169, 209, 749])
}

移动平均¶

第一步，我们需要计算 pollutants_A 在 24 小时窗口内的移动平均，以及 pollutants_B 在 8 小时窗口内的移动平均。我们将使用np.cumsum和切片索引编写一个简单的 moving_mean 函数来实现这一点。

为了确保两个集合的长度相同，我们将根据 pollutants_A_24hr_avg 的长度截断 pollutants_B_8hr_avg。这也能确保我们在同一时间段内拥有所有污染物的浓度。

def moving_mean(a, n):
    ret = np.cumsum(a, dtype=float, axis=0)
    ret[n:] = ret[n:] - ret[:-n]
    return ret[n - 1:] / n

pollutants_A_24hr_avg = moving_mean(pollutants_A, 24)
pollutants_B_8hr_avg = moving_mean(pollutants_B, 8)[-(pollutants_A_24hr_avg.shape[0]):]

现在，我们可以使用np.concatenate将两个集合连接起来，形成所有平均浓度的单一数据集。请注意，我们必须按列连接数组，因此我们传递 axis=1 参数。

pollutants = np.concatenate((pollutants_A_24hr_avg, pollutants_B_8hr_avg), axis=1)

子指数¶

每个污染物的子指数根据 AQI 和标准断点范围之间的线性关系，根据上述公式计算。

Ip = \dfrac{\text{IHi – ILo}}{\text{BPHi – BPLo}}\cdot{\text{Cp – BPLo}} + \text{ILo}

(2)

compute_indices 函数首先使用我们之前创建的 AQI 和 breakpoints 数组，为输入浓度和污染物获取正确的 AQI 类别上限和下限以及断点浓度。然后，它将这些值馈入公式以计算子指数。

def compute_indices(pol, con):
    bp = breakpoints[pol]
    
    if pol == 'CO':
        inc = 0.1
    else:
        inc = 1
    
    if bp[0] <= con < bp[1]:
        Bl = bp[0]
        Bh = bp[1] - inc
        Ih = AQI[1] - inc
        Il = AQI[0]

    elif bp[1] <= con < bp[2]:
        Bl = bp[1]
        Bh = bp[2] - inc
        Ih = AQI[2] - inc
        Il = AQI[1]

    elif bp[2] <= con < bp[3]:
        Bl = bp[2]
        Bh = bp[3] - inc
        Ih = AQI[3] - inc
        Il = AQI[2]

    elif bp[3] <= con < bp[4]:
        Bl = bp[3]
        Bh = bp[4] - inc
        Ih = AQI[4] - inc
        Il = AQI[3]

    elif bp[4] <= con < bp[5]:
        Bl = bp[4]
        Bh = bp[5] - inc
        Ih = AQI[5] - inc
        Il = AQI[4]

    elif bp[5] <= con:
        Bl = bp[5]
        Bh = bp[5] + bp[4] - (2 * inc)
        Ih = AQI[6]
        Il = AQI[5]

    else:
        print("Concentration out of range!")
        
    return ((Ih - Il) / (Bh - Bl)) * (con - Bl) + Il

我们将使用np.vectorize来利用矢量化的概念。这意味着我们不必自己循环遍历污染物数组的每个元素。矢量化是 NumPy 的关键优势之一。

vcompute_indices = np.vectorize(compute_indices)

通过调用我们矢量化的函数 vcompute_indices 来计算每个污染物的子指数。为了获得具有原始形状的数组，我们使用np.stack。

sub_indices = np.stack((vcompute_indices('PM2.5', pollutants[..., 0]),
                        vcompute_indices('PM10', pollutants[..., 1]),
                        vcompute_indices('NO2', pollutants[..., 2]),
                        vcompute_indices('NH3', pollutants[..., 3]),
                        vcompute_indices('SO2', pollutants[..., 4]),
                        vcompute_indices('CO', pollutants[..., 5]),
                        vcompute_indices('O3', pollutants[..., 6])), axis=1)

空气质量指数¶

使用np.max，我们找出每个时期的最大子指数，这就是我们的空气质量指数！

aqi_array = np.max(sub_indices, axis=1)

至此，我们得到了 2019 年 6 月 1 日至 2020 年 6 月 30 日每小时的 AQI。请注意，尽管我们最初的数据是从 5 月 31 日开始的，但在移动平均阶段我们将其截断了。

对 AQI 进行配对学生 t 检验¶

假设检验是一种描述性统计形式，用于帮助我们根据数据做出决策。从计算出的 AQI 数据中，我们想找出在实施封锁前后平均 AQI 是否存在统计学上的显著差异。我们将使用单侧（左尾）配对学生 t 检验来计算两个检验统计量——t 统计量和p 值。然后，我们将这些值与相应的临界值进行比较以做出决策。

Normal distribution plot showing area of rejection in one-tailed test (left tailed)

抽样¶

我们现在将从原始数据集中导入 datetime 列到一个datetime64 数据类型数组中。我们将使用此数组索引 AQI 数组并获取数据集的子集。

datetime = np.loadtxt("air-quality-data.csv", dtype='M8[h]', delimiter=",",
                         skiprows=1, usecols=(0, ))[-(pollutants_A_24hr_avg.shape[0]):]

由于德里从 2020 年 3 月 24 日开始全面封锁，因此封锁后子集的时间范围是 2020 年 3 月 24 日至 2020 年 6 月 30 日。封锁前子集的时间范围是 3 月 24 日之前的相同时间段。

after_lock = aqi_array[np.where(datetime >= np.datetime64('2020-03-24T00'))]

before_lock = aqi_array[np.where(datetime <= np.datetime64('2020-03-21T00'))][-(after_lock.shape[0]):]

print(after_lock.shape)
print(before_lock.shape)

(2376,)
(2376,)

为了确保我们的样本近似正态分布，我们抽取了大小为 n = 30 的样本。before_sample 和 after_sample 是在全面封锁之前和之后抽取的一组随机观测值。我们使用random.Generator.choice来生成样本。

rng = default_rng()

before_sample = rng.choice(before_lock, size=30, replace=False)
after_sample = rng.choice(after_lock, size=30, replace=False)

定义假设¶

我们假设封锁前后样本均值之间没有显著差异。这将是原假设。备择假设是均值之间存在显著差异，并且 AQI 有所改善。数学上表示为：

$H_{0}: \mu_\text{after-before} = 0$
$H_{a}: \mu_\text{after-before} < 0$

计算检验统计量¶

我们将使用 t 统计量来评估我们的假设，甚至从它计算出 p 值。t 统计量的公式是

t = \frac{\mu_\text{after-before}}{\sqrt{\sigma^{2}/n}}

(3)

其中，

$\mu_\text{after-before}$ = 样本的均值差
$\sigma^{2}$ = 均值差的方差
$n$ = 样本大小

def t_test(x, y):
    diff = y - x
    var = np.var(diff, ddof=1)
    num = np.mean(diff)
    denom = np.sqrt(var / len(x))
    return np.divide(num, denom)

t_value = t_test(before_sample, after_sample)

对于 p 值，我们将使用 SciPy 的 stats.distributions.t.cdf() 函数。它接受两个参数：t 统计量和自由度 (dof)。dof 的公式是 n - 1。

dof = len(before_sample) - 1

p_value = stats.distributions.t.cdf(t_value, dof)

print("The t value is {} and the p value is {}.".format(t_value, p_value))

The t value is -9.822796518960033 and the p value is 4.942942624434147e-11.

`t` 值和 `p` 值意味着什么？¶

现在我们将计算出的检验统计量与临界检验统计量进行比较。临界 t 值是通过查找 t 分布表来计算的。

Table of selected t values at different confidence levels. T value for 29 dof at 95% confidence level is highlighted with a yellow square

从上表可以看出，在 95% 置信水平下，对于 29 个 dof，临界值为 1.699。由于我们使用的是左尾检验，所以我们的临界值为 -1.699。显然，计算出的 t 值小于临界值，因此我们可以安全地拒绝原假设。

临界 p 值，表示为 $\alpha$ ，通常选择为 0.05，对应 95% 的置信水平。如果计算出的 p 值小于 $\alpha$ ，则可以安全地拒绝原假设。显然，我们的 p 值远小于 $\alpha$ ，因此我们可以拒绝原假设。

请注意，这并不意味着我们可以接受备择假设。它只告诉我们没有足够的证据拒绝 $H_{a}$ 。换句话说，我们未能拒绝备择假设，因此，它可能是真的。

实践中...¶

对于时间序列数据分析，使用pandas库是更好的选择。
SciPy 的 stats 模块提供了 stats.ttest_rel 函数，可用于获取 t 统计量和 p 值。
在现实生活中，数据通常不是正态分布的。对于这种非正态数据，有诸如 Wilcoxon 检验之类的检验方法。

进一步阅读¶

您可以根据给定数据的特征选择各种统计检验。请阅读统计数据分布的入门介绍以了解更多信息。
存在各种版本的学生 t 检验，您可以根据您的需求选择。