绘制分形

分形是美丽且引人注目的数学形态，它们通常可以通过一套相对简单的指令来创建。在自然界中，它们可以出现在各种地方，例如海岸线、贝壳和蕨类植物，甚至被用于制造某些类型的天线。分形的数学概念已经存在相当长一段时间了，但直到 20 世纪 70 年代，随着计算机图形学的进步和一些偶然的发现，研究人员才开始真正欣赏到分形所拥有的令人费解的可视化效果，例如 Benoît Mandelbrot。

今天我们将学习如何绘制这些美丽的可视化效果，并开始自己探索，同时熟悉分形的数学原理，并利用强大的 NumPy 通用函数高效地执行必要的计算。

您将做什么¶

编写一个用于绘制各种 Julia 集合的函数
创建曼德布洛特集合的可视化
编写一个计算牛顿分形的函数
尝试各种通用分形类型的变体

您将学到什么¶

对分形数学原理有更好的直观理解
对 NumPy 通用函数和布尔索引有基本了解
在 NumPy 中处理复数的基本知识
如何创建自己独特的分形可视化

您将需要什么¶

Matplotlib
mpl_toolkits API 中的 make_axis_locatable 函数

可以按如下方式导入

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable

对 Python、NumPy 和 matplotlib 有一些熟悉度
了解初等数学函数，如指数、正弦、多项式等
对复数有非常基本的了解会很有帮助
了解导数可能有帮助

热身¶

为了对分形有一个直观的理解，我们将从一个例子开始。

考虑以下方程

$f(z) = z^2 -1$

其中 z 是一个复数（即形式为 $a + bi$ ）

为了方便起见，我们将为此编写一个 Python 函数

def f(z):
    return np.square(z) - 1

请注意，我们使用的平方函数是 **NumPy 通用函数** 的一个例子；我们稍后会回到这个决定的意义。

为了直观地了解函数的行为，我们可以尝试代入一些不同的值。

对于 $z = 0$ ，我们预期得到-1:

f(0)

np.int64(-1)

由于我们在设计中使用了通用函数，我们可以同时计算多个输入

z = [4, 1-0.2j, 1.6]
f(z)

array([15. +0.j , -0.04-0.4j, 1.56+0.j ])

有些值会增长，有些值会收缩，有些值变化不大。

为了在大范围内查看函数的行为，我们可以将函数应用于复平面的一个子集并绘制结果。要创建我们的子集（或网格），我们可以利用 meshgrid 函数。

x, y = np.meshgrid(np.linspace(-10, 10, 20), np.linspace(-10, 10, 20))
mesh = x + (1j * y)  # Make mesh of complex plane

现在我们将函数应用于网格中的每个值。由于我们在设计中使用了通用函数，这意味着我们可以一次性传入整个网格。这非常方便，原因有二：它减少了需要编写的代码量，并且极大地提高了效率（因为通用函数在其计算中利用了系统级别的 C 编程）。

这里我们使用 **3D 散点图** 绘制函数经过一次“迭代”后网格中每个元素的绝对值（或模）。

output = np.abs(f(mesh))  # Take the absolute value of the output (for plotting)

fig = plt.figure()
ax = plt.axes(projection='3d')

ax.scatter(x, y, output, alpha=0.2)

ax.set_xlabel('Real axis')
ax.set_ylabel('Imaginary axis')
ax.set_zlabel('Absolute value')
ax.set_title('One Iteration: $ f(z) = z^2 - 1$');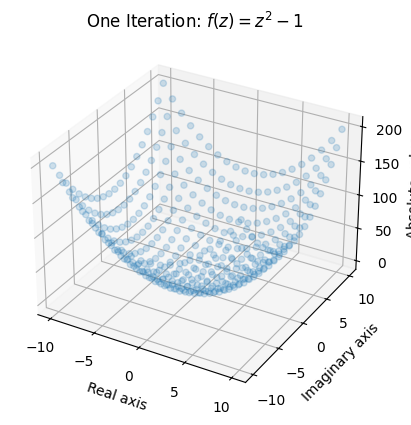

这给了我们关于函数一次迭代的作用的大致了解。某些区域（尤其是在最接近 $(0,0i)$ 的区域）保持相对较小，而其他区域则增长得相当可观。请注意，通过取绝对值，我们丢失了关于输出的信息，但这是我们能够绘制图形的唯一方法。

让我们看看将函数应用到网格 2 次会发生什么

output = np.abs(f(f(mesh)))

ax = plt.axes(projection='3d')

ax.scatter(x, y, output, alpha=0.2)

ax.set_xlabel('Real axis')
ax.set_ylabel('Imaginary axis')
ax.set_zlabel('Absolute value')
ax.set_title('Two Iterations: $ f(z) = z^2 - 1$');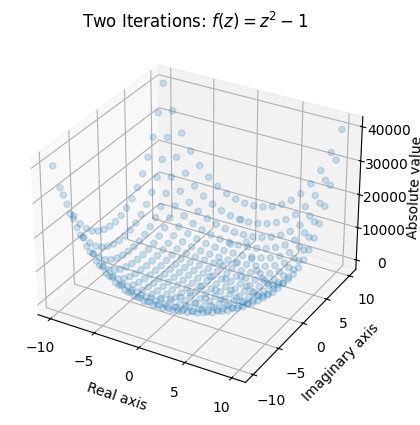

同样，我们看到原点附近的数值保持较小，而绝对值（或模）较大的数值则“爆炸”。

乍一看，它的行为似乎很正常，甚至可能显得平淡无奇。分形通常比表面看起来有更多的内涵；当我们开始应用更多次迭代时，奇异的行为才会显现出来。

考虑三个复数

$z_1 = 0.4 + 0.4i$ ,

$z_2 = z_1 + 0.1$ ,

$z_3 = z_1 + 0.1i$

鉴于前两个图的形状，我们预期这些值在应用迭代时会保持在原点附近。让我们看看将 10 次迭代应用于每个值会发生什么

selected_values = np.array([0.4 + 0.4j, 0.41 + 0.4j, 0.4 + 0.41j])
num_iter = 9

outputs = np.zeros((num_iter+1, selected_values.shape[0]), dtype=complex)
outputs[0] = selected_values

for i in range(num_iter):
    outputs[i+1] = f(outputs[i])  # Apply 10 iterations, save each output

fig, axes = plt.subplots(1, selected_values.shape[0], figsize=(16, 6))
axes[1].set_xlabel('Real axis')
axes[0].set_ylabel('Imaginary axis')

for ax, data in zip(axes, outputs.T):
    cycle = ax.scatter(data.real, data.imag, c=range(data.shape[0]), alpha=0.6)
    ax.set_title(f'Mapping of iterations on {data[0]}')

fig.colorbar(cycle, ax=axes, location="bottom", label='Iteration');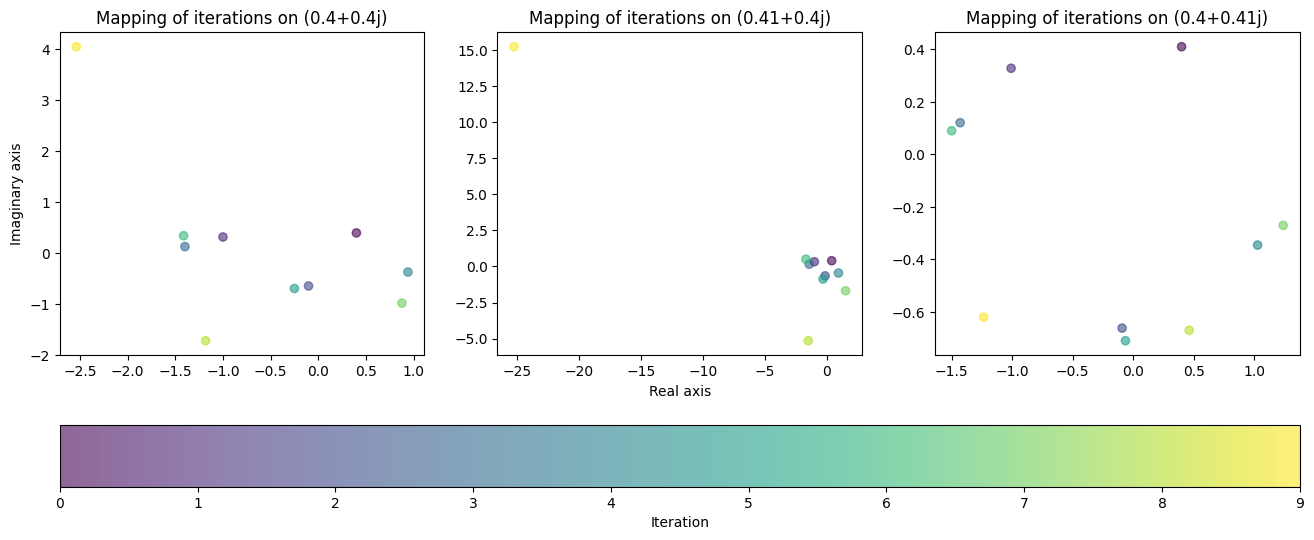

出乎意料的是，函数的行为远未能符合我们的假设。这是分形所具有的混沌行为的一个典型例子。在前两个图中，“爆炸”的值在最后一次迭代时，远远超出了它之前所处的范围。而第三个图则保持在一个接近原点的很小的范围内，尽管数值的微小变化却产生了完全不同的行为。

这引出了一个极其重要的问题：**在数值“爆炸”（发散）之前，每个值可以应用多少次迭代？**

从前两个图中可以看出，数值离原点的距离越远，它们通常爆炸得越快。尽管较小数值的行为（如 $z_1, z_2, z_3$ ) 是不确定的，但我们可以假设，如果一个值超出了到原点的一定距离（例如 2），那么它注定会发散。我们将这个阈值称为 **半径**。

这使我们能够量化特定值的函数行为，而无需执行太多计算。一旦超过半径，我们就可以停止迭代，这为我们提供了一种回答我们提出的问题的方法。如果我们统计发散前应用的计算次数，我们就能获得关于函数行为的洞察，而这种洞察很难通过其他方式跟踪。

当然，我们可以做得更好，设计一个对整个网格执行该过程的函数。

def divergence_rate(mesh, num_iter=10, radius=2):

    z = mesh.copy()
    diverge_len = np.zeros(mesh.shape)  # Keep tally of the number of iterations

    # Iterate on element if and only if |element| < radius (Otherwise assume divergence)
    for i in range(num_iter):
        conv_mask = np.abs(z) < radius
        diverge_len[conv_mask] += 1
        z[conv_mask] = f(z[conv_mask])

    return diverge_len

此函数的行为乍一看可能令人困惑，因此解释一些符号会有所帮助。

我们的目标是迭代网格中的每个值，并统计发散前的迭代次数。由于某些值发散的速度比其他值快，因此我们需要一种只迭代绝对值足够小的值的过程。我们还希望一旦值超过半径就停止计数。为此，我们可以使用 **布尔索引**，这是 NumPy 的一项功能，当与通用函数配对时，它是无与伦比的。布尔索引允许在不诉诸于循环检查每个数组值的情况下，有条件地对 NumPy 数组执行操作。

在我们的例子中，我们使用循环将迭代应用于函数 $f(z) = z^2 -1$ 并进行计数。使用布尔索引，我们只将迭代应用于绝对值小于 2 的值。

这样一来，我们就可以绘制我们的第一个分形了！我们将使用 **imshow** 函数来创建计数的颜色编码可视化。

x, y = np.meshgrid(np.linspace(-2, 2, 400), np.linspace(-2, 2, 400))
mesh = x + (1j * y)

output = divergence_rate(mesh)

fig = plt.figure(figsize=(5, 5))
ax = plt.axes()

ax.set_title('$f(z) = z^2 -1$')
ax.set_xlabel('Real axis')
ax.set_ylabel('Imaginary axis')

im = ax.imshow(output, extent=[-2, 2, -2, 2])
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.1)
plt.colorbar(im, cax=cax, label='Number of iterations');

这张令人惊叹的视觉效果传达了函数行为的复杂性。黄色区域代表保持较小的值，而紫色区域代表发散的值。收敛和发散值边界上出现的精美图案，当你意识到它是由如此简单的函数创建的时，就更加迷人了。

Julia 集合¶

我们刚刚探索的是一个特定 Julia 集合的分形可视化示例。

考虑函数 $f(z) = z^2 + c$ 其中 $c$ 是一个复数。 $c$ 的 **填充 Julia 集合** 是函数在 $f(z)$ 处收敛的所有复数 z 的集合。同样，填充 Julia 集合的边界就是我们称之为 **Julia 集合** 的。

为了能够访问更广泛的“Julia 分形”，我们可以编写一个函数，允许传入不同的 $c$ 值

def julia(mesh, c=-1, num_iter=10, radius=2):

    z = mesh.copy()
    diverge_len = np.zeros(z.shape)

    for i in range(num_iter):
        conv_mask = np.abs(z) < radius
        z[conv_mask] = np.square(z[conv_mask]) + c
        diverge_len[conv_mask] += 1

    return diverge_len

为了使我们的工作更轻松，我们将创建几个将在其余示例中重用的网格

x, y = np.meshgrid(np.linspace(-1, 1, 400), np.linspace(-1, 1, 400))
small_mesh = x + (1j * y)

x, y = np.meshgrid(np.linspace(-2, 2, 400), np.linspace(-2, 2, 400))
mesh = x + (1j * y)

我们还将编写一个函数，用于创建分形图

def plot_fractal(fractal, title='Fractal', figsize=(6, 6), cmap='rainbow', extent=[-2, 2, -2, 2]):

    plt.figure(figsize=figsize)
    ax = plt.axes()

    ax.set_title(f'${title}$')
    ax.set_xlabel('Real axis')
    ax.set_ylabel('Imaginary axis')

    im = ax.imshow(fractal, extent=extent, cmap=cmap)
    divider = make_axes_locatable(ax)
    cax = divider.append_axes("right", size="5%", pad=0.1)
    plt.colorbar(im, cax=cax, label='Number of iterations')

使用我们新定义的函数，我们可以快速再次绘制第一个分形图

output = julia(mesh, num_iter=15)
kwargs = {'title': 'f(z) = z^2 -1'}

plot_fractal(output, **kwargs);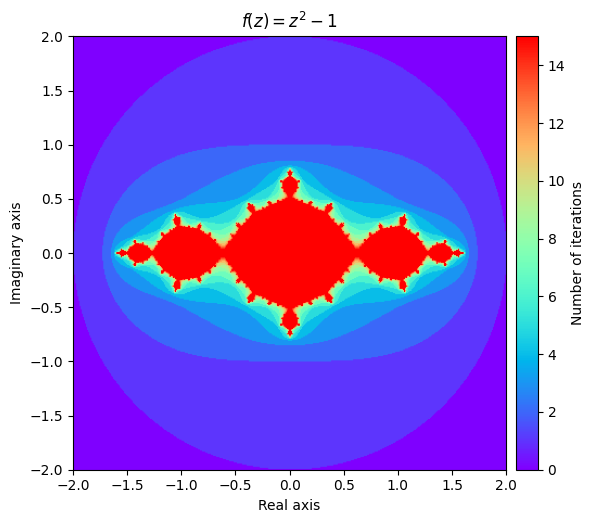

我们还可以通过尝试不同的 $c$ 值来探索一些不同的 Julia 集合。它对分形形状的影响程度可能令人惊讶。

例如，设置 $c = \frac{\pi}{10}$ 会产生一个非常优美的云状形状，而设置 c = $-\frac{3}{4} + 0.4i$ 会产生完全不同的图案。

output = julia(mesh, c=np.pi/10, num_iter=20)
kwargs = {'title': r'f(z) = z^2 + \dfrac{\pi}{10}', 'cmap': 'plasma'}

plot_fractal(output, **kwargs);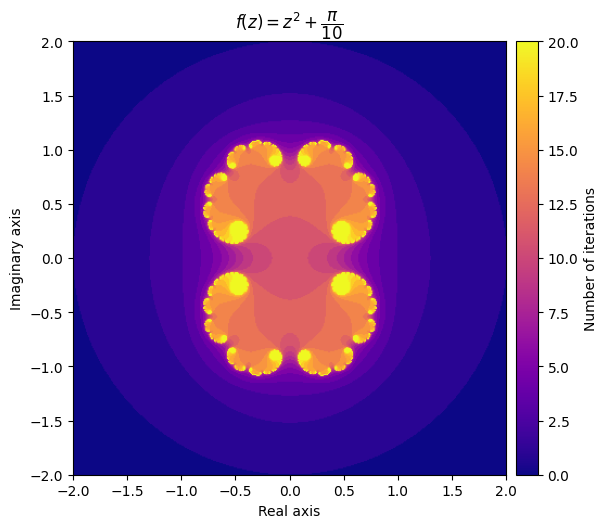

output = julia(mesh, c=-0.75 + 0.4j, num_iter=20)
kwargs = {'title': r'f(z) = z^2 - \dfrac{3}{4} + 0.4i', 'cmap': 'Greens_r'}

plot_fractal(output, **kwargs);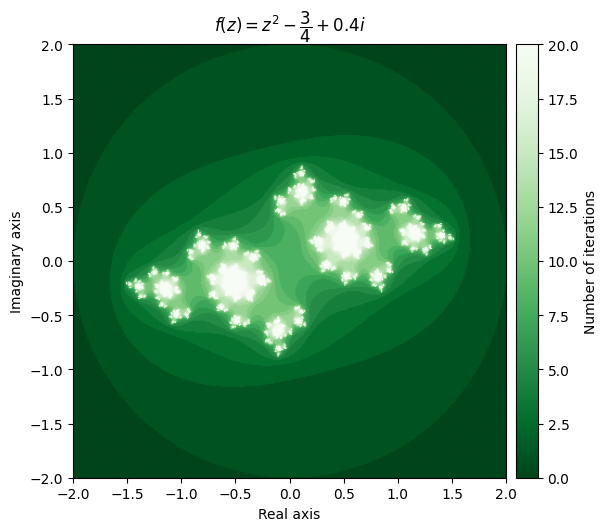

曼德布洛特集合¶

与 Julia 集合密切相关的是著名的 **曼德布洛特集合**，它的定义略有不同。同样，我们定义 $f(z) = z^2 + c$ 其中 $c$ 是一个复数，但这次我们关注的是我们对 $c$ 的选择。我们说 $c$ 是曼德布洛特集合的元素，如果函数在 $z = 0$ 处收敛。等价的定义是， $c$ 是曼德布洛特集合的元素，如果 $f(c)$ 可以无限次迭代而不“爆炸”。我们将对 Julia 函数进行轻微调整（并相应重命名），以便我们可以绘制曼德布洛特集合的可视化，该集合具有优雅的分形图案。

def mandelbrot(mesh, num_iter=10, radius=2):

    c = mesh.copy()
    z = np.zeros(mesh.shape, dtype=np.complex128)
    diverge_len = np.zeros(z.shape)

    for i in range(num_iter):
        conv_mask = np.abs(z) < radius
        z[conv_mask] = np.square(z[conv_mask]) + c[conv_mask]
        diverge_len[conv_mask] += 1

    return diverge_len

output = mandelbrot(mesh, num_iter=50)
kwargs = {'title': 'Mandelbrot \\ set', 'cmap': 'hot'}

plot_fractal(output, **kwargs);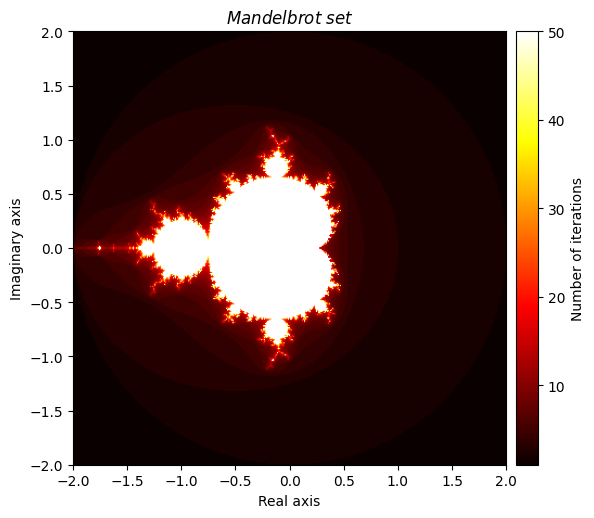

Julia 集合的泛化¶

我们可以通过提供一个参数来进一步泛化 Julia 函数，以指定我们希望传入哪个通用函数。这将允许我们绘制形式为 $f(z) = g(z) + c$ 的分形，其中 g 是由我们选择的通用函数。

def general_julia(mesh, c=-1, f=np.square, num_iter=100, radius=2):

    z = mesh.copy()
    diverge_len = np.zeros(z.shape)

    for i in range(num_iter):
        conv_mask = np.abs(z) < radius
        z[conv_mask] = f(z[conv_mask]) + c
        diverge_len[conv_mask] += 1

    return diverge_len

使用我们的通用 Julia 函数可以绘制的一组很酷的分形是形式为 $f(z) = z^n + c$ 的分形，其中 $n$ 是某个正整数。一个非常酷的模式是，“伸出”的区域数量与迭代过程中将函数提高的次数相匹配。

fig, axes = plt.subplots(2, 3, figsize=(8, 8))
base_degree = 2

for deg, ax in enumerate(axes.ravel()):
    degree = base_degree + deg
    power = lambda z: np.power(z, degree)  # Create power function for current degree

    diverge_len = general_julia(mesh, f=power, num_iter=15)
    ax.imshow(diverge_len, extent=[-2, 2, -2, 2], cmap='binary')
    ax.set_title(f'$f(z) = z^{degree} -1$')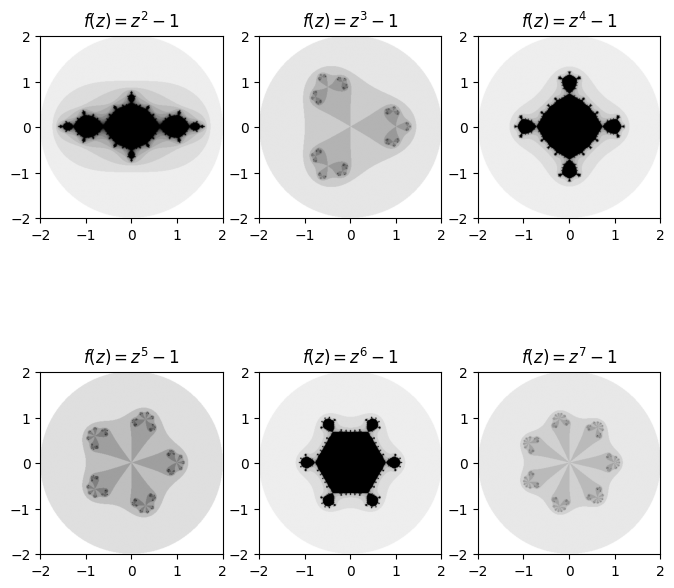

不用说，通过调整输入的函数、 $c$ 的值、迭代次数、半径，甚至网格密度和颜色选择，都可以进行大量的探索。

牛顿分形¶

牛顿分形是一类特殊的分形，其中迭代涉及将函数（通常是多项式）与其导数的比值加减到输入值。数学上，它可以表示为

$z := z - \frac{f(z)}{f'(z)}$

我们将定义一个通用版本的分形，通过传入我们选择的函数来实现不同的变体绘图。

def newton_fractal(mesh, f, df, num_iter=10, r=2):

    z = mesh.copy()
    diverge_len = np.zeros(z.shape)

    for i in range(num_iter):
        conv_mask = np.abs(z) < r
        pz = f(z[conv_mask])
        dp = df(z[conv_mask])
        z[conv_mask] = z[conv_mask] - pz/dp
        diverge_len[conv_mask] += 1

    return diverge_len

现在我们可以尝试一些不同的函数。对于多项式，我们可以使用 NumPy Polynomial 类轻松创建我们的绘图，该类内置了计算导数的功能。

例如，让我们尝试一个高次多项式

p = np.polynomial.Polynomial([-16, 0, 0, 0, 15, 0, 0, 0, 1])
p

加载中...

其导数为

p.deriv()

加载中...

output = newton_fractal(mesh, p, p.deriv(), num_iter=15, r=2)
kwargs = {'title': r'f(z) = z - \dfrac{(z^8 + 15z^4 - 16)}{(8z^7 + 60z^3)}', 'cmap': 'copper'}

plot_fractal(output, **kwargs)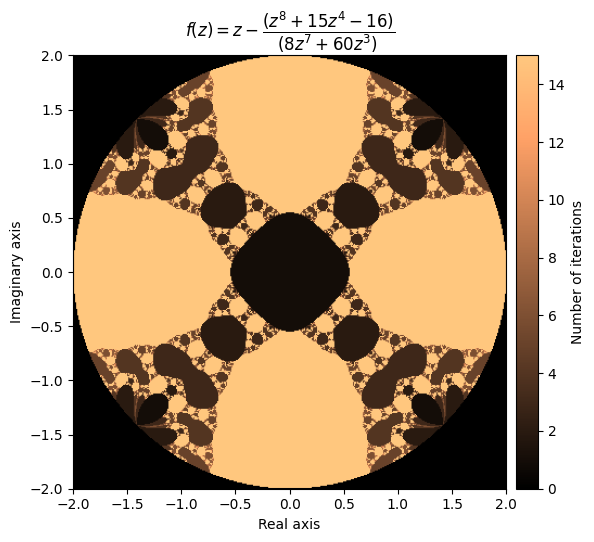

太棒了！让我们再试一个

f(z) = $tan^2(z)$

$\frac{df}{dz} = 2 \cdot tan(z) sec^2(z) =\frac{2 \cdot tan(z)}{cos^2(z)}$

这使得 $\frac{f(z)}{f'(z)} = tan^2(z) \cdot \frac{cos^2(z)}{2 \cdot tan(z)} = \frac{tan(z)\cdot cos^2(z)}{2} = \frac{sin(z)\cdot cos(z)}{2}$

def f_tan(z):
    return np.square(np.tan(z))


def d_tan(z):
    return 2*np.tan(z) / np.square(np.cos(z))

output = newton_fractal(mesh, f_tan, d_tan, num_iter=15, r=50)
kwargs = {'title': r'f(z) = z - \dfrac{sin(z)cos(z)}{2}', 'cmap': 'binary'}

plot_fractal(output, **kwargs);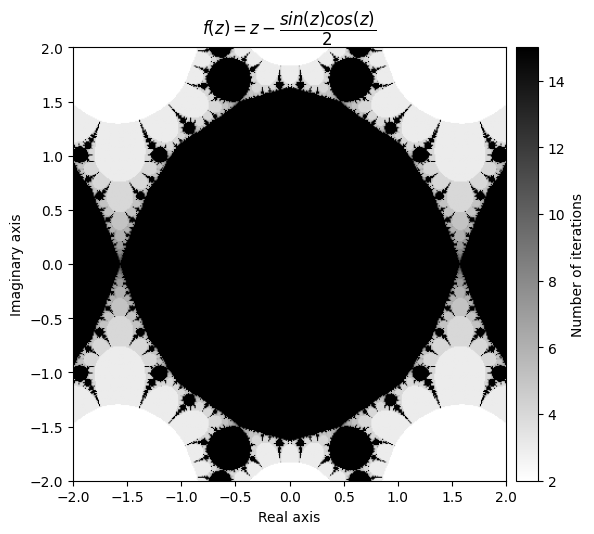

请注意，有时你需要调整半径才能得到一个漂亮的、看起来像分形的图像。

最后，我们可以大胆地选择我们的函数

$f(z) = \sum_{i=1}^{10} sin^i(z)$

$\frac{df}{dz} = \sum_{i=1}^{10} i \cdot sin^{i-1}(z) \cdot cos(z)$

def sin_sum(z, n=10):
    total = np.zeros(z.size, dtype=z.dtype)
    for i in range(1, n+1):
        total += np.power(np.sin(z), i)
    return total


def d_sin_sum(z, n=10):
    total = np.zeros(z.size, dtype=z.dtype)
    for i in range(1, n+1):
        total += i * np.power(np.sin(z), i-1) * np.cos(z)
    return total

我们将这个命名为“Wacky fractal”，因为它的方程不容易写在标题里。

output = newton_fractal(small_mesh, sin_sum, d_sin_sum, num_iter=10, r=1)
kwargs = {'title': 'Wacky \\ fractal', 'figsize': (6, 6), 'extent': [-1, 1, -1, 1], 'cmap': 'terrain'}

plot_fractal(output, **kwargs)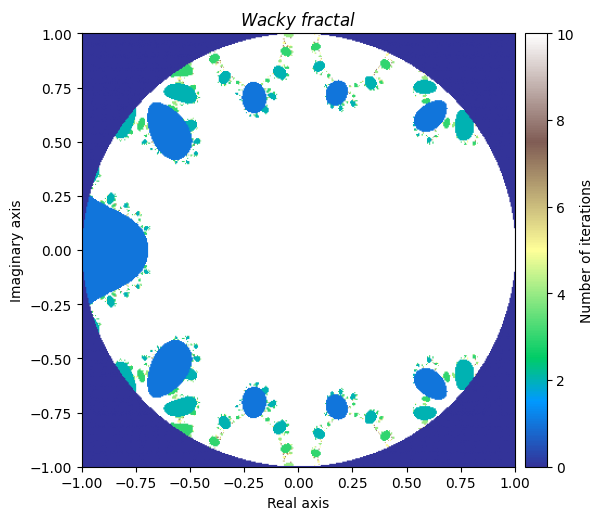

这些分形彼此之间既截然不同又惊人的相似，这真是太迷人了。这让我们进入最后一个部分。

创建你自己的分形¶

分形之所以更令人兴奋，是因为一旦你熟悉了基础知识，还有很多可以探索的。现在，我们将通过探索一些可以用来实验创建独特分形的不同方法来结束我们的教程。我鼓励你自己尝试一些（如果你还没有这样做的话）。

第一个可以实验的地方是广义朱利亚集的函数，我们可以尝试传入不同的函数作为参数。

让我们从选择开始

$f(z) = tan(z^2)$

def f(z):
    return np.tan(np.square(z))

output = general_julia(mesh, f=f, num_iter=15, radius=2.1)
kwargs = {'title': 'f(z) = tan(z^2)', 'cmap': 'gist_stern'}

plot_fractal(output, **kwargs);

如果我们把定义的函数组合在一个正弦函数里面会发生什么？

让我们来定义

$g(z) = sin(f(z)) = sin(tan(z^2))$

def g(z):
    return np.sin(f(z))

output = general_julia(mesh, f=g, num_iter=15, radius=2.1)
kwargs = {'title': 'g(z) = sin(tan(z^2))', 'cmap': 'plasma_r'}

plot_fractal(output, **kwargs);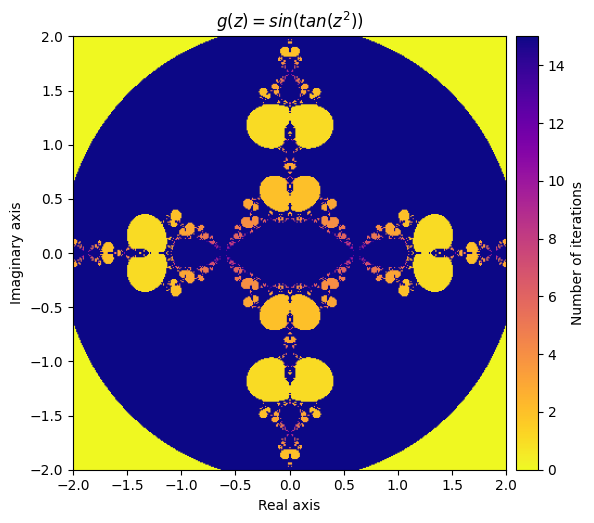

接下来，让我们创建一个函数，该函数在每次迭代中对输入应用 f 和 g，并将结果相加

$h(z) = f(z) + g(z) = tan(z^2) + sin(tan(z^2))$

def h(z):
    return f(z) + g(z)

output = general_julia(small_mesh, f=h, num_iter=10, radius=2.1)
kwargs = {'title': 'h(z) = tan(z^2) + sin(tan(z^2))', 'figsize': (7, 7), 'extent': [-1, 1, -1, 1], 'cmap': 'jet'}

plot_fractal(output, **kwargs);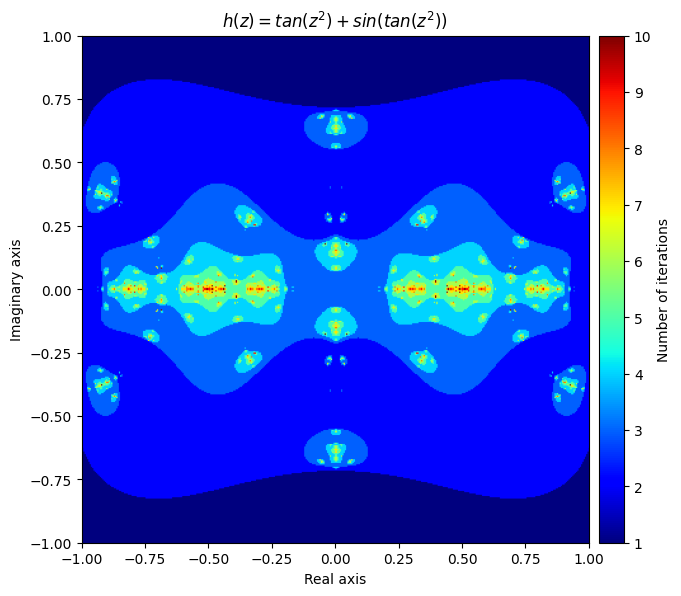

你甚至可以通过自己的错误创造出美丽的分形。这是一个在计算牛顿分形导数时出错而意外产生的例子

def accident(z):
    return z - (2 * np.power(np.tan(z), 2) / (np.sin(z) * np.cos(z)))

output = general_julia(mesh, f=accident, num_iter=15, c=0, radius=np.pi)
kwargs = {'title': 'Accidental \\ fractal', 'cmap': 'Blues'}

plot_fractal(output, **kwargs);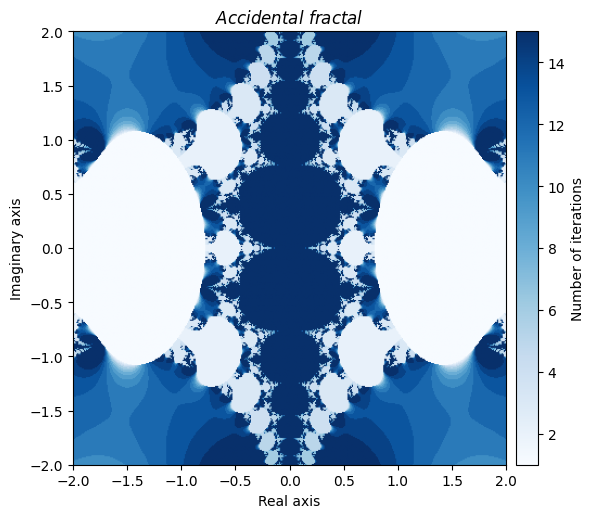

Needless to say, there are a nearly endless supply of interesting fractal creations that can be made just by playing around with various combinations of NumPy universal functions and by tinkering with the parameters.

结论¶

今天我们学到了很多关于生成分形的东西。我们看到了复杂的、需要多次迭代的分形是如何通过通用函数高效计算的。我们还利用了布尔索引，这使得计算量减少，而无需单独验证每个值。最后，我们对分形本身有了很多了解。回顾一下：

分形图像是通过对一组值进行函数迭代而创建的，并记录每个值通过某个阈值所需的时间。
图像中的颜色对应于值的计数。
对于 $c$ 的填充朱利亚集由所有复数 z 组成，其中 $f(z) = z^2 + c$ 收敛。
对于 $c$ 的朱利亚集是由填充朱利亚集的边界组成的一组复数。
曼德尔布罗集是所有值 $c$ 使得 $f(z) = z^2 + c$ 收敛于 0
牛顿分形使用形式为 $f(z) = z - \frac{p(z)}{p'(z)}$ 的函数
分形图像会随着您调整迭代次数、收敛半径、网格大小、颜色、函数选择和参数选择而变化

自己动手¶

尝试修改广义朱利亚集函数的参数，可以尝试调整常数、迭代次数、函数选择、半径和颜色选择。
访问“豪斯多夫维度分形列表”维基百科页面（在“拓展阅读”部分有链接），并尝试为你在此教程中未提及的分形编写一个函数。