使用NumPy确定静力平衡

在分析物理结构时，理解维持其稳定的力学至关重要。施加在地板、梁或其他任何结构上的力会产生反作用力和力矩。这些反作用力是结构在不破裂的情况下抵抗运动的力量。当结构在受到力的作用时但未发生移动时，牛顿第二定律指出，系统中所有方向的加速度和力的总和都必须为零。您可以使用NumPy数组来表示和解决此概念。

您将做什么：¶

在本教程中，您将使用NumPy创建向量和力矩，并使用NumPy数组。
解决涉及电缆和地板支撑结构的力学问题。
编写NumPy矩阵来隔离未知数。
使用NumPy函数执行线性代数运算。

您将学到什么：¶

如何使用NumPy表示点、向量和力矩。
如何找到向量的法线。
使用NumPy计算矩阵运算。

您将需要：¶

NumPy
Matplotlib

使用以下命令导入

import numpy as np
import matplotlib.pyplot as plt

在本教程中，您将使用以下NumPy工具

np.linalg.norm：此函数用于确定向量幅度的度量。
np.cross：此函数接受两个矩阵并产生叉积。

使用牛顿第二定律求解平衡¶

您的模型由一个承受合力和合力矩的梁组成。您可以通过牛顿第二定律开始分析此系统。

\sum{\text{force}} = \text{mass} \times \text{acceleration}.

(1)

为了简化示例，假设它们是静止的，加速度为 $=0$ 。由于我们的系统存在于三维空间中，请考虑在每个维度上施加的力。这意味着您可以将这些力表示为向量。对于由物体质心与其作用点之间的距离产生的力矩，您也会得出相同的结论。

假设力 $F$ 表示为三维向量。

F = (F_x, F_y, F_z)

(2)

其中每个分量代表施加在相应方向上的力的幅度。也假设向量中的每个分量

r = (r_x, r_y, r_z)

(3)

是施加每个力分量的点与系统质心之间的距离。那么，力矩可以计算为

r \times F = (r_x, r_y, r_z) \times (F_x, F_y, F_z).

(4)

从一些简单的力向量示例开始。

forceA = np.array([1, 0, 0])
forceB = np.array([0, 1, 0])
print("Force A =", forceA)
print("Force B =", forceB)

Force A = [1 0 0]
Force B = [0 1 0]

这定义了forceA为一个在 $x$ 方向上幅度为1的向量，forceB为一个在 $y$ 方向上幅度为1的向量。

为了更好地理解这些力如何相互作用，可视化它们可能会有帮助。Matplotlib是一个包含可视化工具的库，可用于此目的。Quiver图将用于演示三维向量，但该库也可用于二维演示。

fig = plt.figure()

d3 = fig.add_subplot(projection="3d")

d3.set_xlim(-1, 1)
d3.set_ylim(-1, 1)
d3.set_zlim(-1, 1)

x, y, z = np.array([0, 0, 0])  # defining the point of application.  Make it the origin

u, v, w = forceA  # breaking the force vector into individual components
d3.quiver(x, y, z, u, v, w, color="r", label="forceA")

u, v, w = forceB
d3.quiver(x, y, z, u, v, w, color="b", label="forceB")

plt.legend()
plt.show()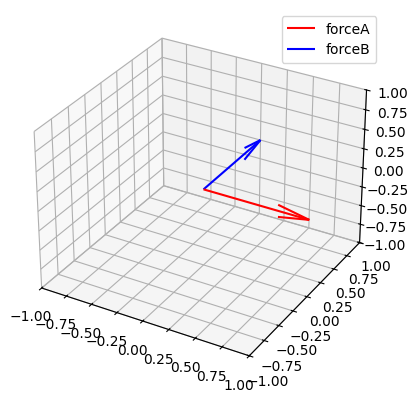

有两个力从同一点出发。为了简化这个问题，您可以将它们相加以找到力的总和。请注意，forceA和forceB都是三维向量，在NumPy中表示为具有三个分量的数组。由于NumPy旨在简化和优化向量之间的运算，因此您可以轻松地计算这两个向量的总和，如下所示：

forceC = forceA + forceB
print("Force C =", forceC)

Force C = [1 1 0]

力C现在作为代表A和B的单一力存在。您可以绘制它来查看结果。

fig = plt.figure()

d3 = fig.add_subplot(projection="3d")

d3.set_xlim(-1, 1)
d3.set_ylim(-1, 1)
d3.set_zlim(-1, 1)

x, y, z = np.array([0, 0, 0])

u, v, w = forceA
d3.quiver(x, y, z, u, v, w, color="r", label="forceA")
u, v, w = forceB
d3.quiver(x, y, z, u, v, w, color="b", label="forceB")
u, v, w = forceC
d3.quiver(x, y, z, u, v, w, color="g", label="forceC")

plt.legend()
plt.show()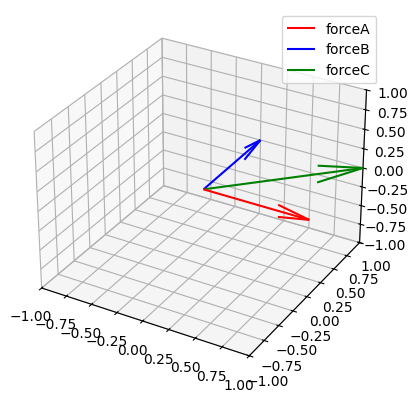

然而，目标是实现平衡。这意味着您希望您的合力为 $(0, 0, 0)$ ，否则您的物体将经历加速度。因此，需要有另一个力来抵消之前的力。

您可以将此问题写成 $A+B+R=0$ ，其中 $R$ 是解决问题的反作用力。

在此示例中，这意味着

(1, 0, 0) + (0, 1, 0) + (R_x, R_y, R_z) = (0, 0, 0)

(5)

分解为 $x$ 、 $y$ 和 $z$ 分量，得到

\begin{cases} 1+0+R_x=0\\ 0+1+R_y=0\\ 0+0+R_z=0 \end{cases}

(6)

求解 $R_x$ 、 $R_y$ 、和 $R_z$ 得到向量 $R$ 为 $(-1, -1, 0)$ 。

如果绘制出来，先前示例中的力将被抵消。只有当没有剩余力时，系统才被认为处于平衡状态。

R = np.array([-1, -1, 0])

fig = plt.figure()

d3.set_xlim(-1, 1)
d3.set_ylim(-1, 1)
d3.set_zlim(-1, 1)

d3 = fig.add_subplot(projection="3d")

x, y, z = np.array([0, 0, 0])

u, v, w = forceA + forceB + R  # add them all together for sum of forces
d3.quiver(x, y, z, u, v, w)

plt.show()

空图表示没有外力。这表示系统处于平衡状态。

以力矩之和求解平衡¶

接下来，让我们看一个更复杂的应用。当所有力不作用于同一点时，会产生力矩。

与力类似，这些力矩的总和也必须为零，否则会产生旋转加速度。与力的总和类似，这为空间中的三个坐标方向中的每一个创建了一个线性方程。

一个简单的例子是固定在地下的静止杆上施加的力。杆不动，因此它必须施加反作用力。杆也不会旋转，因此它也必须产生反作用力矩。求解反作用力和反作用力矩。

假设在距离杆基部2米处垂直施加一个5N的力。

f = 5  # Force in newtons
L = 2  # Length of the pole

R = 0 - f
M = 0 - f * L
print("Reaction force =", R)
print("Reaction moment =", M)

Reaction force = -5
Reaction moment = -10

寻找具有物理特性的值¶

假设力不是垂直作用在梁上，而是通过一根也固定在地面的绳索施加在我们杆件上。考虑到绳索的张力，您只需要知道这些物体的物理位置就可以解决这个问题。

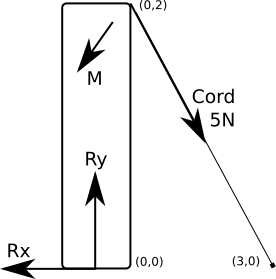
为了响应作用在杆件上的力，基座产生了 x 和 y 方向的反作用力以及一个反作用力矩。

将杆件的基座设为原点。现在，假设绳索固定在地面上，距离原点 x 方向 3 米，并固定在杆件上，距离原点 z 方向 2 米高。

将这些空间点定义为 NumPy 数组，然后使用这些数组来查找方向向量。

poleBase = np.array([0, 0, 0])
cordBase = np.array([3, 0, 0])
cordConnection = np.array([0, 0, 2])

poleDirection = cordConnection - poleBase
print("Pole direction =", poleDirection)
cordDirection = cordBase - cordConnection
print("Cord direction =", cordDirection)

Pole direction = [0 0 2]
Cord direction = [ 3  0 -2]

为了在力相关中使用这些向量，您需要将它们转换为单位向量。单位向量的模长为一，只表示力的方向。

cordUnit = cordDirection / np.linalg.norm(cordDirection)
print("Cord unit vector =", cordUnit)

Cord unit vector = [ 0.83205029  0.         -0.5547002 ]

然后，您可以通过将此方向乘以力的大小来找到力向量。

假设绳索的张力为 5N。

cordTension = 5
forceCord = cordUnit * cordTension
print("Force from the cord =", forceCord)

Force from the cord = [ 4.16025147  0.         -2.77350098]

为了找到力矩，您需要力向量和半径的叉乘。

momentCord = np.cross(forceCord, poleDirection)
print("Moment from the cord =", momentCord)

Moment from the cord = [ 0.         -8.32050294  0.        ]

现在，您只需要找到反作用力和力矩。

equilibrium = np.array([0, 0, 0])
R = equilibrium - forceCord
M = equilibrium - momentCord
print("Reaction force =", R)
print("Reaction moment =", M)

Reaction force = [-4.16025147  0.          2.77350098]
Reaction moment = [0.         8.32050294 0.        ]

另一个例子¶

让我们看一个稍微复杂一些的模型。在本例中，您将观察一个带有两条缆绳和一个作用力的梁。这次您需要找到绳索的张力以及梁的反作用力。（来源：Vector Mechanics for Engineers: Statics and Dynamics，问题 4.106）

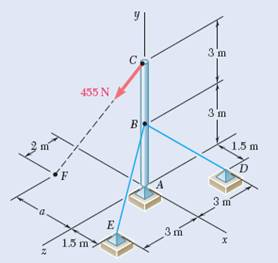
定义距离 a 为 3 米。

和之前一样，首先将每个相关点的位置定义为数组。

A = np.array([0, 0, 0])
B = np.array([0, 3, 0])
C = np.array([0, 6, 0])
D = np.array([1.5, 0, -3])
E = np.array([1.5, 0, 3])
F = np.array([-3, 0, 2])

从这些方程开始，您通过确定单位向量来确定向量方向。

AB = B - C
AC = C - A
BD = D - B
BE = E - B
CF = F - C

UnitBD = BD / np.linalg.norm(BD)
UnitBE = BE / np.linalg.norm(BE)
UnitCF = CF / np.linalg.norm(CF)

RadBD = np.cross(AB, UnitBD)
RadBE = np.cross(AB, UnitBE)
RadCF = np.cross(AC, UnitCF)

这允许您将作用在系统上的张力（T）和反作用力（R）表示为

Unknown column alignment: \nobreakspace at position 1: \̲n̲o̲b̲r̲e̲a̲k̲s̲p̲a̲c̲e̲

\left[
\begin{array}
~1/3 & 1/3 & 1 & 0 & 0\\
-2/3 & -2/3 & 0 & 1 & 0\\
-2/3 & 2/3 & 0 & 0 & 1\\
\end{array}
\right]
\left[
\begin{array}
~T_{BD}\\
T_{BE}\\
R_{x}\\
R_{y}\\
R_{z}\\
\end{array}
\right]
=
\left[
\begin{array}
~195\\
390\\
-130\\
\end{array}
\right]

以及力矩为

Unknown column alignment: \nobreakspace at position 1: \̲n̲o̲b̲r̲e̲a̲k̲s̲p̲a̲c̲e̲

\left[
\begin{array}
~2 & -2\\
1 & 1\\
\end{array}
\right]
\left[
\begin{array}
~T_{BD}\\
T_{BE}\\
\end{array}
\right]
=
\left[
\begin{array}
~780\\
1170\\
\end{array}
\right]

其中 $T$ 是相应绳索的张力， $R$ 是相应方向的反作用力。然后您就有六个方程

$\sum F_{x} = 0 = T_{BE}/3+T_{BD}/3-195+R_{x}$

$\sum F_{y} = 0 = (-\frac{2}{3})T_{BE}-\frac{2}{3}T_{BD}-390+R_{y}$

$\sum F_{z} = 0 = (-\frac{2}{3})T_{BE}+\frac{2}{3}T_{BD}+130+R_{z}$

$\sum M_{x} = 0 = 780+2T_{BE}-2T_{BD}$

$\sum M_{z} = 0 = 1170-T_{BE}-T_{BD}$

现在您有五个未知数和五个方程，可以求解

$\ T_{BD} = 780N$

$\ T_{BE} = 390N$

$\ R_{x} = -195N$

$\ R_{y} = 1170N$

$\ R_{z} = 130N$

总结¶

您已经学会了如何使用数组来表示三维空间中的点、力和力矩。数组中的每个条目都可以用来表示分解为方向分量的物理属性。然后，可以使用 NumPy 函数轻松地对其进行操作。

其他应用¶

这个相同的过程可以应用于动力学问题或任何维度的任何问题。本教程中的示例假设了三维静力平衡问题。这些方法可以轻松地用于更广泛的问题。更多或更少的维度需要更大或更小的数组来表示。在存在加速度的系统中，速度和加速度也可以类似地表示为向量。