如何创建具有等间距值的数组#

NumPy 中有几个函数在应用上相似，但结果略有不同，如果不确定何时以及如何使用它们，可能会导致混淆。本指南旨在列出这些函数并描述其推荐用法。

此处提及的函数有

一维域（区间）#

`linspace` vs. `arange`#

numpy.linspace 和 numpy.arange 都提供了将区间（一维域）划分为等长子区间的方法。这些划分将根据所选的起始点、结束点和**步长**（子区间的长度）而变化。

**如果您需要整数步长，请使用** numpy.arange。

numpy.arange 依靠步长来确定返回数组中的元素数量，其中不包括终点。这由 arange 的 step 参数确定。

示例
```
>>> np.arange(0, 10, 2)  # np.arange(start, stop, step)
array([0, 2, 4, 6, 8])
```
参数 start 和 stop 应该是整数或实数，但不是复数。numpy.arange 类似于 Python 内置的 range。

浮点不精确性可能导致 arange 对浮点数的结果产生混淆。在这种情况下，您应该使用 numpy.linspace。
**如果您希望结果包含终点，或者您正在使用非整数步长，请使用** numpy.linspace。

numpy.linspace *可以*包含终点，并根据 num 参数确定步长，该参数指定返回数组中的元素数量。

是否包含终点由一个可选的布尔参数 endpoint 决定，该参数默认为 True。请注意，选择 endpoint=False 将改变步长计算和函数随后的输出。

示例
```
>>> np.linspace(0.1, 0.2, num=5)  # np.linspace(start, stop, num)
array([0.1  , 0.125, 0.15 , 0.175, 0.2  ])
>>> np.linspace(0.1, 0.2, num=5, endpoint=False)
array([0.1, 0.12, 0.14, 0.16, 0.18])
```
numpy.linspace 也可以与复数参数一起使用
```
>>> np.linspace(1+1.j, 4, 5, dtype=np.complex64)
array([1.  +1.j  , 1.75+0.75j, 2.5 +0.5j , 3.25+0.25j, 4.  +0.j  ],
      dtype=complex64)
```

其他示例#

如果在 numpy.arange 中使用浮点值作为 step，可能会出现意外结果。为了避免这种情况，请确保所有浮点转换都在结果计算之后发生。例如，将
```
>>> list(np.arange(0.1,0.4,0.1).round(1))
[0.1, 0.2, 0.3, 0.4]  # endpoint should not be included!
```
替换为
```
>>> list(np.arange(1, 4, 1) / 10.0)
[0.1, 0.2, 0.3]  # expected result
```

请注意

>>> np.arange(0, 1.12, 0.04)
array([0.  , 0.04, 0.08, 0.12, 0.16, 0.2 , 0.24, 0.28, 0.32, 0.36, 0.4 ,
       0.44, 0.48, 0.52, 0.56, 0.6 , 0.64, 0.68, 0.72, 0.76, 0.8 , 0.84,
       0.88, 0.92, 0.96, 1.  , 1.04, 1.08, 1.12])

和

>>> np.arange(0, 1.08, 0.04)
array([0.  , 0.04, 0.08, 0.12, 0.16, 0.2 , 0.24, 0.28, 0.32, 0.36, 0.4 ,
       0.44, 0.48, 0.52, 0.56, 0.6 , 0.64, 0.68, 0.72, 0.76, 0.8 , 0.84,
       0.88, 0.92, 0.96, 1.  , 1.04])

这些差异是由于数字噪声造成的。当使用浮点值时，0 + 0.04 * 28 < 1.12 是可能的，因此 1.12 包含在区间内。实际上，情况正是如此

>>> 1.12/0.04
28.000000000000004

但是 0 + 0.04 * 27 >= 1.08，所以 1.08 被排除在外

>>> 1.08/0.04
27.0

或者，您可以使用 np.arange(0, 28)*0.04，它将始终精确控制终点，因为它是一个整数

>>> np.arange(0, 28)*0.04
array([0.  , 0.04, 0.08, 0.12, 0.16, 0.2 , 0.24, 0.28, 0.32, 0.36, 0.4 ,
       0.44, 0.48, 0.52, 0.56, 0.6 , 0.64, 0.68, 0.72, 0.76, 0.8 , 0.84,
       0.88, 0.92, 0.96, 1.  , 1.04, 1.08])

`geomspace` 和 `logspace`#

numpy.geomspace 类似于 numpy.linspace，但数字在对数刻度上等间距（几何级数）。结果包含终点。

示例

>>> np.geomspace(2, 3, num=5)
array([2.        , 2.21336384, 2.44948974, 2.71080601, 3.        ])

numpy.logspace 类似于 numpy.geomspace，但起始点和结束点以对数形式指定（默认以 10 为底）

>>> np.logspace(2, 3, num=5)
array([ 100.        ,  177.827941  ,  316.22776602,  562.34132519, 1000.        ])

在线性空间中，序列从 base ** start（base 的 start 次方）开始，以 base ** stop 结束

>>> np.logspace(2, 3, num=5, base=2)
array([4.        , 4.75682846, 5.65685425, 6.72717132, 8.        ])

N 维域#

N 维域可以划分为*网格*。这可以通过以下函数之一完成。

`meshgrid`#

numpy.meshgrid 的目的是从一组一维坐标数组中创建矩形网格。

给定数组

>>> x = np.array([0, 1, 2, 3])
>>> y = np.array([0, 1, 2, 3, 4, 5])

meshgrid 将创建两个坐标数组，可用于生成确定此网格的坐标对。

>>> xx, yy = np.meshgrid(x, y)
>>> xx
array([[0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3],
       [0, 1, 2, 3]])
>>> yy
array([[0, 0, 0, 0],
       [1, 1, 1, 1],
       [2, 2, 2, 2],
       [3, 3, 3, 3],
       [4, 4, 4, 4],
       [5, 5, 5, 5]])

>>> import matplotlib.pyplot as plt
>>> plt.plot(xx, yy, marker='.', color='k', linestyle='none')

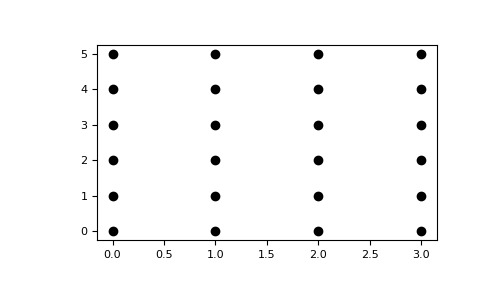
`mgrid`#

numpy.mgrid 可用作创建网格的快捷方式。它不是一个函数，但当被索引时，它会返回一个多维网格。

>>> xx, yy = np.meshgrid(np.array([0, 1, 2, 3]), np.array([0, 1, 2, 3, 4, 5]))
>>> xx.T, yy.T
(array([[0, 0, 0, 0, 0, 0],
        [1, 1, 1, 1, 1, 1],
        [2, 2, 2, 2, 2, 2],
        [3, 3, 3, 3, 3, 3]]),
 array([[0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5]]))

>>> np.mgrid[0:4, 0:6]
array([[[0, 0, 0, 0, 0, 0],
        [1, 1, 1, 1, 1, 1],
        [2, 2, 2, 2, 2, 2],
        [3, 3, 3, 3, 3, 3]],

       [[0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5],
        [0, 1, 2, 3, 4, 5]]])

`ogrid`#

与 numpy.mgrid 类似，numpy.ogrid 返回一个*开放*的多维网格。这意味着当它被索引时，每个返回数组只有一个维度大于 1。这避免了重复数据，从而节省了内存，这通常是可取的。

这些稀疏坐标网格旨在与广播（Broadcasting）一起使用。当所有坐标都在一个表达式中使用时，广播仍然会产生一个完全维度的结果数组。

>>> np.ogrid[0:4, 0:6]
(array([[0],
        [1],
        [2],
        [3]]), array([[0, 1, 2, 3, 4, 5]]))

此处描述的所有三种方法都可用于在网格上评估函数值。

>>> g = np.ogrid[0:4, 0:6]
>>> zg = np.sqrt(g[0]**2 + g[1]**2)
>>> g[0].shape, g[1].shape, zg.shape
((4, 1), (1, 6), (4, 6))
>>> m = np.mgrid[0:4, 0:6]
>>> zm = np.sqrt(m[0]**2 + m[1]**2)
>>> np.array_equal(zm, zg)
True

如何创建具有等间距值的数组#

一维域（区间）#

linspace vs. arange#

其他示例#

geomspace 和 logspace#

N 维域#

meshgrid#

mgrid#

ogrid#

`linspace` vs. `arange`#

`geomspace` 和 `logspace`#

`meshgrid`#

`mgrid`#

`ogrid`#