numpy.percentile#

numpy.percentile(a, q, axis=None, out=None, overwrite_input=False, method='linear', keepdims=False, *, weights=None, interpolation=None)[source]#

沿指定轴计算数据的第 q 个百分位数。

返回数组元素的第 q 个百分位数。

参数：

a实数的 array_like

输入数组或可转换为数组的对象。

q浮点数的 array_like

要计算的百分位数的百分比或百分比序列。值必须在 0 到 100 之间（包括 0 和 100）。

axis{int, int 元组, None}, 可选

计算百分位数的轴或轴。默认值是沿数组的扁平化版本计算百分位数。

版本 1.9.0 中变更：支持轴的元组

outndarray, 可选

放置结果的备用输出数组。它必须与预期输出具有相同的形状和缓冲区长度，但类型（输出的类型）将在必要时强制转换。

overwrite_inputbool, 可选

如果为 True，则允许修改输入数组 a，以节省内存。在这种情况下，此函数完成后的输入 a 的内容是未定义的。

methodstr, 可选

此参数指定用于估计百分位数的方法。存在许多不同的方法，其中一些是 NumPy 独有的。有关解释，请参见注释。按 H&F 论文 [1] 中概述的 R 类型排序的选项是

‘inverted_cdf’
‘averaged_inverted_cdf’
‘closest_observation’
‘interpolated_inverted_cdf’
‘hazen’
‘weibull’
‘linear’ (默认)
‘median_unbiased’
‘normal_unbiased’

前三种方法是不连续的。NumPy 还定义了以下默认 'linear' (7.) 选项的不连续变体

‘lower’
‘higher’，
‘midpoint’
‘nearest’

版本 1.22.0 中变更：此参数以前称为“interpolation”，并且仅提供“linear”默认值和最后四个选项。

keepdimsbool, 可选

如果将其设置为 True，则减少的轴将保留在结果中，作为大小为 1 的维度。使用此选项，结果将针对原始数组 a 正确广播。

版本 1.9.0 中新增。

weightsarray_like, 可选: 与 a 中的值关联的权重数组。每个 a 中的值都根据其关联权重对百分位数做出贡献。权重数组可以是一维（在这种情况下，其长度必须是 a 沿给定轴的大小）或与 a 形状相同。如果 weights=None，则假定 a 中的所有数据都具有等于 1 的权重。仅 method=”inverted_cdf” 支持权重。有关更多详细信息，请参见注释。

版本 2.0.0 中新增。

interpolationstr, 可选

method 关键字参数的已弃用名称。

版本 1.22.0 中弃用。

返回值：

percentile标量或 ndarray: 如果 q 是单个百分位数并且 axis=None，则结果为标量。如果给出多个百分位数，则结果的第一轴对应于百分位数。其他轴是在减少 a 之后剩下的轴。如果输入包含小于 float64 的整数或浮点数，则输出数据类型为 float64。否则，输出数据类型与输入相同。如果指定了 out，则返回该数组。

另请参见

mean
median: 等效于 percentile(..., 50)
nanpercentile
quantile: 等效于 percentile，除了 q 在 [0, 1] 范围内。

注释

百分比为 q 的 numpy.percentile 的行为与参数为 q/100 的 numpy.quantile 相同。有关更多信息，请参见 numpy.quantile。

参考文献

[1]

R. J. Hyndman 和 Y. Fan，“统计软件包中的样本分位数”，《美国统计学家》，50(4)，第 361-365 页，1996 年

示例

>>> import numpy as np
>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10,  7,  4],
       [ 3,  2,  1]])
>>> np.percentile(a, 50)
3.5
>>> np.percentile(a, 50, axis=0)
array([6.5, 4.5, 2.5])
>>> np.percentile(a, 50, axis=1)
array([7.,  2.])
>>> np.percentile(a, 50, axis=1, keepdims=True)
array([[7.],
       [2.]])

>>> m = np.percentile(a, 50, axis=0)
>>> out = np.zeros_like(m)
>>> np.percentile(a, 50, axis=0, out=out)
array([6.5, 4.5, 2.5])
>>> m
array([6.5, 4.5, 2.5])

>>> b = a.copy()
>>> np.percentile(b, 50, axis=1, overwrite_input=True)
array([7.,  2.])
>>> assert not np.all(a == b)

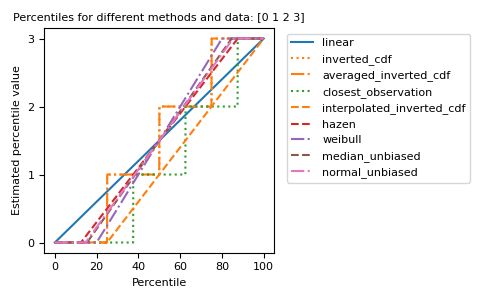
不同的方法可以用图形方式可视化

import matplotlib.pyplot as plt

a = np.arange(4)
p = np.linspace(0, 100, 6001)
ax = plt.gca()
lines = [
    ('linear', '-', 'C0'),
    ('inverted_cdf', ':', 'C1'),
    # Almost the same as `inverted_cdf`:
    ('averaged_inverted_cdf', '-.', 'C1'),
    ('closest_observation', ':', 'C2'),
    ('interpolated_inverted_cdf', '--', 'C1'),
    ('hazen', '--', 'C3'),
    ('weibull', '-.', 'C4'),
    ('median_unbiased', '--', 'C5'),
    ('normal_unbiased', '-.', 'C6'),
    ]
for method, style, color in lines:
    ax.plot(
        p, np.percentile(a, p, method=method),
        label=method, linestyle=style, color=color)
ax.set(
    title='Percentiles for different methods and data: ' + str(a),
    xlabel='Percentile',
    ylabel='Estimated percentile value',
    yticks=a)
ax.legend(bbox_to_anchor=(1.03, 1))
plt.tight_layout()
plt.show()